Exponential Functions for MATH 140
Exam Relevance for MATH 140
Exponential functions are foundational in MATH 140. Properties and graphs should be second nature.
Introduction
Imagine a contractor offers you a choice for a month-long job:
Option A: $1,000 per day
Option B: 1 penny on day 1, doubled each day (2¢ on day 2, 4¢ on day 3, 8¢ on day 4, ...)
Which would you choose?
Option A gives you $30,000 for the month. Sounds pretty good, right?
Let's see what happens with Option B:
| Day | That Day's Pay | Running Total |
|---|---|---|
| 1 | 1¢ | 1¢ |
| 5 | 16¢ | 31¢ |
| 10 | $5.12 | $10.23 |
| 15 | $163.84 | $327.67 |
| 20 | $5,242.88 | $10,485.75 |
| 25 | $167,772.16 | $335,544.31 |
| 30 | $5,368,709.12 | $10,737,418.23 |
That humble penny grew into over $10.7 million. Meanwhile, Option A gave you $30,000.
This is the shocking power of exponential growth—and exactly what you'll master in this lesson.
What is an Exponential Function?
An exponential function has the variable in the exponent:
$$f(x) = a^x$$
where $a > 0$ and $a \neq 1$.
This might look like a small change — moving the variable from the base to the exponent — but as you just saw, it creates dramatically different behavior. Exponential functions grow (or decay) faster than any polynomial.
The key examples:
- $f(x) = 2^x$ — doubles every time $x$ increases by 1
- $g(x) = 10^x$ — multiplies by 10 every time $x$ increases by 1
- $h(x) = e^x$ — the most important exponential function in calculus (more on this later!)
Why the Variable's Position Matters
Let's compare two similar-looking functions:
| Function | Name | Variable is in the... |
|---|---|---|
| $f(x) = x^2$ | Power function (polynomial) | Base |
| $g(x) = 2^x$ | Exponential function | Exponent |
These look similar but behave completely differently!
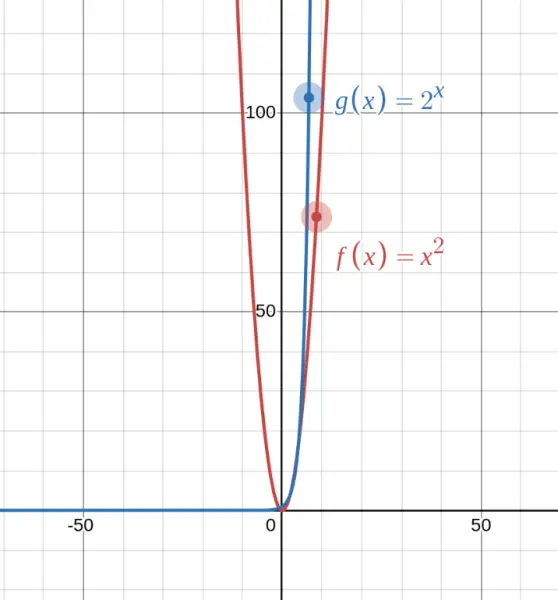
At first, $x^2$ is bigger. But watch what happens as $x$ grows — the exponential function $2^x$ eventually rockets past the polynomial and keeps accelerating. By $x = 10$, we have $x^2 = 100$ but $2^x = 1024$. By $x = 20$, we have $x^2 = 400$ but $2^x = 1,048,576$!
This is the key insight: exponential growth is fundamentally faster than polynomial growth.
Understanding Exponential Growth
Let's build intuition with a simple example: $f(x) = 2^x$
| $x$ | $2^x$ | What's happening |
|---|---|---|
| 0 | 1 | Starting point |
| 1 | 2 | Doubled! |
| 2 | 4 | Doubled again! |
| 3 | 8 | Still doubling... |
| 4 | 16 | Every step doubles |
| 5 | 32 | |
| 10 | 1,024 | Over a thousand |
| 20 | 1,048,576 | Over a million! |
The pattern: every time $x$ increases by 1, the output multiplies by 2.
This "constant multiplier" behavior is what defines exponential growth. It's why:
- Populations can explode so quickly
- Viruses spread so rapidly
- Compound interest makes money grow faster over time
- A piece of paper folded 42 times would reach the moon!
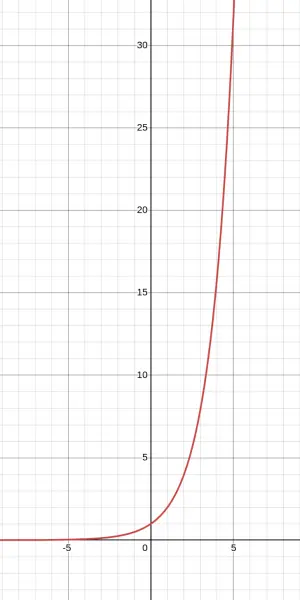
Notice the shape: relatively flat on the left, then curving upward more and more steeply. This "hockey stick" shape is the signature of exponential growth.
Exponential Decay
What if the base is between 0 and 1? Then we get exponential decay instead of growth.
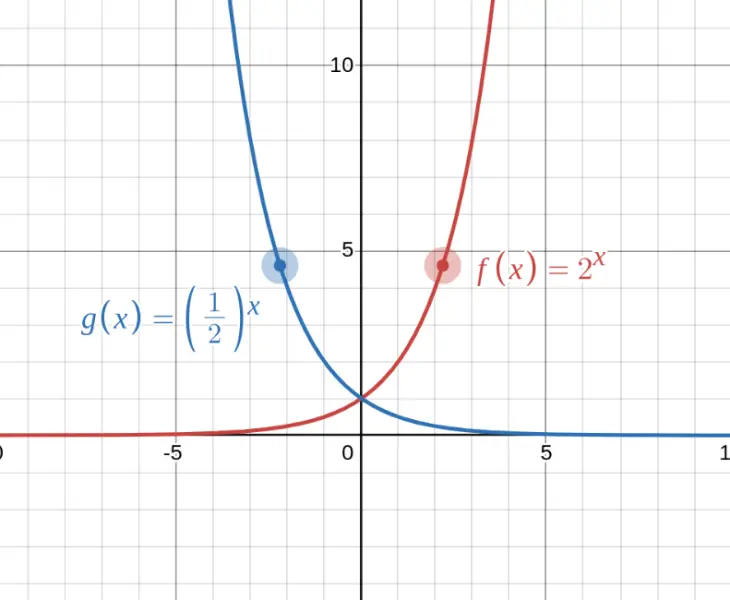
Consider $f(x) = \left(\frac{1}{2}\right)^x$:
| $x$ | $\left(\frac{1}{2}\right)^x$ | What's happening |
|---|---|---|
| 0 | 1 | Starting point |
| 1 | 0.5 | Halved! |
| 2 | 0.25 | Halved again! |
| 3 | 0.125 | Still halving... |
| 4 | 0.0625 | Getting tiny |
| 10 | ≈ 0.001 | Almost zero |
Every time $x$ increases by 1, the output is cut in half.
Why Should You Care About Exponential Decay?
Exponential decay isn't just a math concept — it's how the real world works in countless situations:
Radioactive decay and half-lives: If a radioactive substance has a half-life of 10 years, you can predict exactly how much remains after 50 years, 100 years, or 10,000 years. This is how scientists date ancient artifacts and fossils!
Medicine in your body: When you take medication, your body processes and eliminates it exponentially. Doctors use this to calculate proper dosing — how much to take and how often — so the drug stays in the effective range without becoming toxic.
Cooling and heating: A hot coffee cools quickly at first (big temperature difference with the room), then slower and slower as it approaches room temperature. This is Newton's Law of Cooling — exponential decay in action.
Finance: Depreciation of assets, paying down debt, and understanding inflation all involve exponential decay.
The power this gives you: Once you recognize exponential decay, you can answer questions like:
- "How long until only 10% remains?"
- "What's the half-life?"
- "How much will be left after time $t$?"
These aren't just abstract calculations — they're how pharmacists determine drug dosages, how engineers design safe nuclear facilities, and how investors plan for retirement.
Key observation: $\left(\frac{1}{2}\right)^x = 2^{-x}$. So decay is just growth "going backwards"!
The Key Properties of Exponential Functions
For $f(x) = a^x$ where $a > 0$ and $a \neq 1$:
| Property | What it means |
|---|---|
| Domain | All real numbers (you can plug in any $x$) |
| Range | $(0, \infty)$ — always positive, never zero or negative |
| $y$-intercept | Always $(0, 1)$ because $a^0 = 1$ |
| Horizontal asymptote | $y = 0$ (approaches but never touches the $x$-axis) |
| Always increasing or decreasing | If $a > 1$: always increasing. If $0 < a < 1$: always decreasing |
| One-to-one | Each $y$ value comes from exactly one $x$ value |
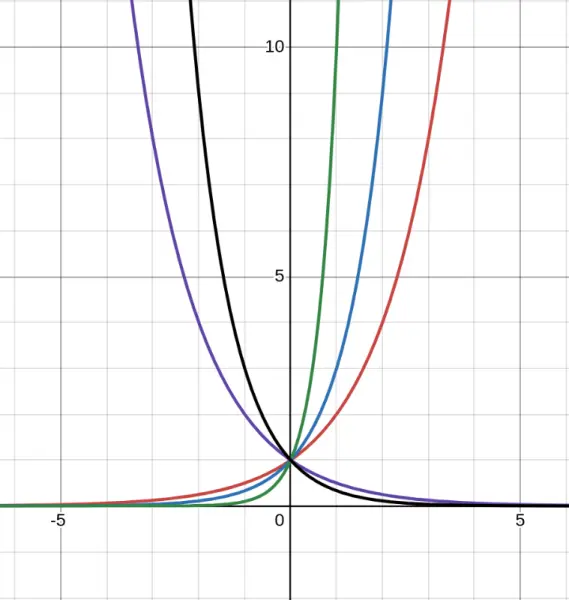
Notice that ALL these curves pass through the point $(0, 1)$. That's because $a^0 = 1$ for any positive $a$.
The Special Number $e$
In calculus, one exponential function stands above all others:
$$f(x) = e^x$$
where $e \approx 2.71828...$
Why is $e$ special? It's the only base where the function equals its own derivative:
$$\frac{d}{dx}[e^x] = e^x$$
This makes $e^x$ incredibly important in calculus — it's the "natural" exponential function. We'll explore this much more when we study derivatives, but for now, just know that $e$ is to exponential functions what $\pi$ is to circles: a fundamental constant that appears everywhere.

The function $e^x$ is sometimes written as $\exp(x)$ — they mean exactly the same thing.
Comparing Exponential to Polynomial
Here's a crucial fact for calculus:
Exponential functions grow faster than ANY polynomial as $x \to \infty$
No matter how high the degree of your polynomial, an exponential function will eventually overtake it.
| As $x \to \infty$ | $x^{10}$ | $x^{100}$ | $2^x$ |
|---|---|---|---|
| $x = 100$ | $10^{20}$ | $10^{200}$ | $2^{100} \approx 10^{30}$ |
| $x = 1000$ | $10^{30}$ | $10^{300}$ | $2^{1000} \approx 10^{301}$ |
Even $x^{100}$ eventually loses to $2^x$!
This is why exponential growth is so powerful — and so dangerous when modeling things like disease spread or resource consumption.
What is NOT an Exponential Function?
Be careful! Not every function with an exponent is exponential.
✗ NOT Exponential Functions:
- $f(x) = x^2$ — variable in base, not exponent (this is a polynomial)
- $g(x) = x^x$ — variable in both base AND exponent (this is something else entirely)
- $h(x) = 2^3$ — no variable at all (this is just the number 8)
- $k(x) = (-2)^x$ — negative base causes problems (undefined for many $x$ values)
✓ ARE Exponential Functions:
- $f(x) = 3^x$ — base is positive constant, variable in exponent ✓
- $g(x) = e^x$ — the natural exponential ✓
- $h(x) = 5 \cdot 2^x$ — exponential with a coefficient ✓
- $k(x) = e^{-x}$ — exponential decay ✓
- $m(x) = 10^{2x}$ — exponential with transformed input ✓
Practice: Identify and Analyze
Problem: Is $f(x) = 5^x$ an exponential function? If so, is it growth or decay?
Yes! The base is 5 (a positive constant) and the variable is in the exponent.
Since $5 > 1$, this is exponential growth.
$$\boxed{\text{Exponential growth}}$$
Problem: Is $g(x) = x^5$ an exponential function?
No! The variable $x$ is in the base, not the exponent.
This is a polynomial (specifically, a power function), not an exponential.
$$\boxed{\text{Not exponential — this is a polynomial}}$$
Problem: Is $h(x) = \left(\frac{2}{3}\right)^x$ growth or decay?
The base is $\frac{2}{3} \approx 0.667$, which is between 0 and 1.
Since $0 < \frac{2}{3} < 1$, this is exponential decay.
$$\boxed{\text{Exponential decay}}$$
Problem: What is the $y$-intercept of $f(x) = 7 \cdot 3^x$?
The $y$-intercept is where $x = 0$:
$f(0) = 7 \cdot 3^0 = 7 \cdot 1 = 7$
$$\boxed{y\text{-intercept: } (0, 7)}$$
Problem: Is it possible that this graph represents an exponential function?
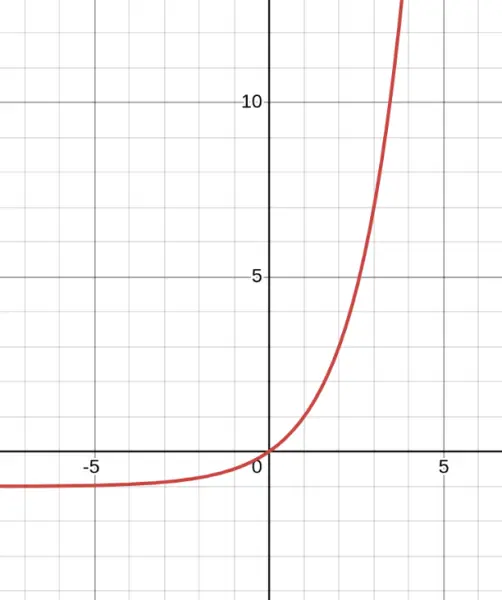
Yes! This looks like an exponential function that has been shifted down.
A basic exponential $a^x$ has a horizontal asymptote at $y = 0$, but this curve levels off at $y = -1$. This is consistent with something like $f(x) = 2^x - 1$.
The key exponential features are still there:
- ✓ Always increasing
- ✓ Has a horizontal asymptote
- ✓ Curves upward more and more steeply
$$\boxed{\text{Yes, this could be a transformed exponential function}}$$
Problem: Is it possible that this graph represents an exponential function?
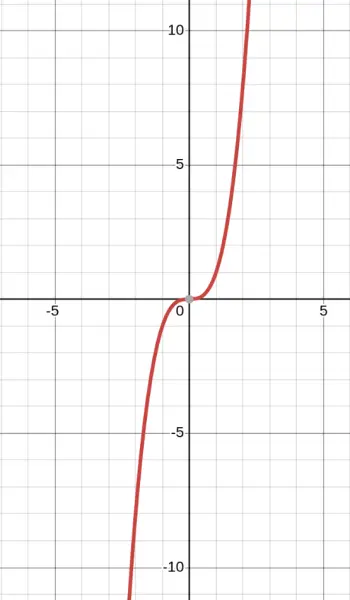
No! Look at the left side of the graph — it goes down to $-\infty$.
Exponential functions are always positive (their range is $(0, \infty)$). They approach $y = 0$ as a horizontal asymptote but never reach zero or go negative.
This graph crosses into negative $y$ values, so it cannot be an exponential function. (It's actually a polynomial — $x^3$.)
$$\boxed{\text{No, exponential functions are always positive}}$$
Common Mistakes and Misunderstandings
❌ Mistake: Confusing $x^a$ with $a^x$
Wrong: "$x^2$ is an exponential function because it has an exponent"
Why it's wrong: Having an exponent isn't enough — the variable must be in the exponent. In $x^2$, the variable is the base and 2 is a constant exponent.
Correct: $x^2$ is a polynomial (power function). An exponential function has a constant base with the variable in the exponent, like $2^x$.
❌ Mistake: Thinking exponential functions can equal zero
Wrong: "Solve $2^x = 0$... so $x = $ something"
Why it's wrong: Exponential functions never equal zero. No matter how negative $x$ gets, $2^x$ approaches 0 but never reaches it.
Correct: The equation $2^x = 0$ has no solution. The range of $2^x$ is $(0, \infty)$ — all positive numbers, but zero is not included.
❌ Mistake: Negative base is fine
Wrong: "$(-3)^x$ is an exponential function with base $-3$"
Why it's wrong: Negative bases cause problems. What is $(-3)^{1/2}$? That's $\sqrt{-3}$, which isn't a real number! Exponential functions require positive bases to be defined for all real $x$.
Correct: Exponential functions have the form $a^x$ where $a > 0$ and $a \neq 1$.
❌ Mistake: Exponential decay goes to negative infinity
Wrong: "As $x \to \infty$, $(1/2)^x \to -\infty$"
Why it's wrong: Exponential decay approaches zero, not negative infinity. The values get smaller and smaller (0.5, 0.25, 0.125, 0.0625...) but stay positive.
Correct: As $x \to \infty$, $\left(\frac{1}{2}\right)^x \to 0^+$ (approaches zero from above). The horizontal asymptote is $y = 0$.
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.