Volumes of Solids of Revolution / Method of Rings for MATH 122
Exam Relevance for MATH 122
May appear as one problem. Setting up disk/washer integrals for volumes.
This skill appears on:
Understanding Volumes of Solids of Revolution
When you rotate a region around an axis, you create a 3D solid. Think of a potter's wheel — spin a shape and you get a vase, bowl, or cylinder. Calculus lets us find the volume of these solids.
The method of rings (also called the disk/washer method) slices the solid perpendicular to the axis of rotation, creating circular cross-sections.
The Disk Method
When a region bounded by $y = f(x)$ and the x-axis is rotated around the x-axis, each vertical slice becomes a disk (a filled circle).
$$V = \int_a^b \pi [f(x)]^2 \, dx$$
Why? Each disk has:
- Radius = $f(x)$ (height of the function)
- Thickness = $dx$
- Area = $\pi r^2 = \pi [f(x)]^2$
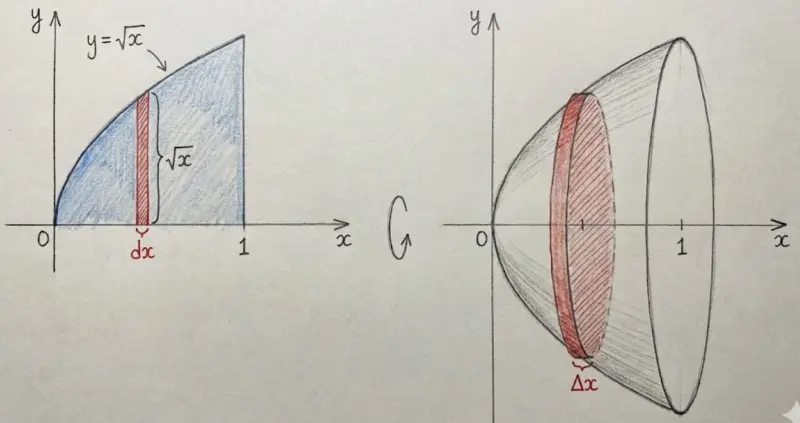
In this visualization, notice how each vertical slice of the region becomes a circular disk when rotated. The radius of each disk equals the function value $f(x)$ at that point.
Problem: Find the volume of the solid formed by rotating $y = x$ from $x = 0$ to $x = 3$ around the x-axis.
This creates a cone with height 3 and base radius 3!
$$V = \int_0^3 \pi x^2 \, dx$$
$$= \pi \left[\frac{x^3}{3}\right]_0^3$$
$$= \pi \cdot \frac{27}{3} = 9\pi$$
$$\boxed{V = 9\pi}$$
Check: The cone formula gives $V = \frac{1}{3}\pi r^2 h = \frac{1}{3}\pi(3)^2(3) = 9\pi$ ✓
Problem: Find the volume of a sphere of radius $r$ by rotating $y = \sqrt{r^2 - x^2}$ around the x-axis.
$$V = \int_{-r}^{r} \pi (\sqrt{r^2 - x^2})^2 \, dx$$
$$= \pi \int_{-r}^{r} (r^2 - x^2) \, dx$$
$$= \pi \left[r^2 x - \frac{x^3}{3}\right]_{-r}^{r}$$
At $x = r$: $r^3 - \frac{r^3}{3} = \frac{2r^3}{3}$
At $x = -r$: $-r^3 + \frac{r^3}{3} = -\frac{2r^3}{3}$
$$V = \pi \left(\frac{2r^3}{3} - \left(-\frac{2r^3}{3}\right)\right) = \pi \cdot \frac{4r^3}{3}$$
$$\boxed{V = \frac{4}{3}\pi r^3}$$
This is the famous sphere volume formula!
The Washer Method
When there's a hole in the middle (the region doesn't touch the axis), each slice is a washer (a disk with a hole).
$$V = \int_a^b \pi \left([R(x)]^2 - [r(x)]^2\right) dx$$
Where:
- $R(x)$ = outer radius (distance from axis to outer curve)
- $r(x)$ = inner radius (distance from axis to inner curve)
Think: Washer area = (big disk) − (small disk) = $\pi R^2 - \pi r^2$
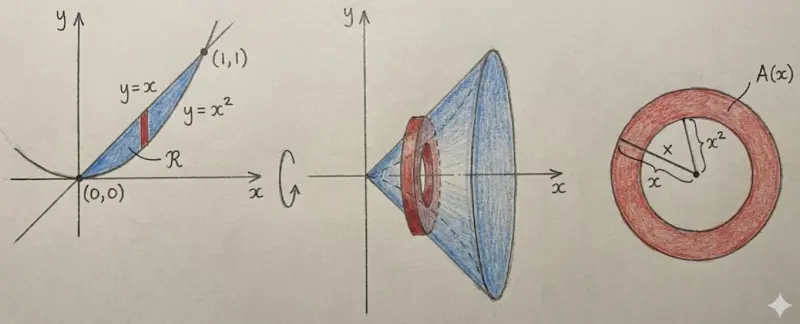
In this visualization, the region between $y = x$ and $y = x^2$ creates a "washer" (ring shape) when rotated. The outer radius comes from the top curve, and the inner radius creates the hole.
Problem: Find the volume when the region between $y = x^2$ and $y = x$ is rotated around the x-axis.
Step 1: Find intersection points
$x^2 = x$ gives $x = 0$ and $x = 1$.
Step 2: Identify outer and inner radii
On $[0, 1]$: $y = x$ is above $y = x^2$.
- Outer radius: $R = x$
- Inner radius: $r = x^2$
Step 3: Set up and evaluate
$$V = \int_0^1 \pi (x^2 - x^4) \, dx$$
$$= \pi \left[\frac{x^3}{3} - \frac{x^5}{5}\right]_0^1$$
$$= \pi \left(\frac{1}{3} - \frac{1}{5}\right) = \pi \cdot \frac{2}{15}$$
$$\boxed{V = \frac{2\pi}{15}}$$
Rotation Around the y-axis
When rotating around the y-axis, express everything in terms of $y$:
$$V = \int_c^d \pi [g(y)]^2 \, dy$$
where $x = g(y)$ is the curve.
Problem: Find the volume when $y = \sqrt{x}$ from $x = 0$ to $x = 4$ is rotated around the y-axis.
Step 1: Rewrite as x = g(y)
$y = \sqrt{x}$ becomes $x = y^2$.
When $x = 0$: $y = 0$. When $x = 4$: $y = 2$.
Step 2: Set up the integral
$$V = \int_0^2 \pi (y^2)^2 \, dy = \pi \int_0^2 y^4 \, dy$$
$$= \pi \left[\frac{y^5}{5}\right]_0^2 = \pi \cdot \frac{32}{5}$$
$$\boxed{V = \frac{32\pi}{5}}$$
Rotation Around Other Lines
When rotating around a line other than an axis, adjust the radius!
Around $y = k$: Radius = $|f(x) - k|$
Around $x = h$: Radius = $|x - h|$ (usually use shell method instead)
Problem: Find the volume when $y = x^2$ from $x = 0$ to $x = 2$ is rotated around $y = -1$.
Step 1: Find the radius
The distance from the curve $y = x^2$ to the line $y = -1$ is:
$$R = x^2 - (-1) = x^2 + 1$$
Step 2: Set up and evaluate
$$V = \int_0^2 \pi (x^2 + 1)^2 \, dx$$
$$= \pi \int_0^2 (x^4 + 2x^2 + 1) \, dx$$
$$= \pi \left[\frac{x^5}{5} + \frac{2x^3}{3} + x\right]_0^2$$
$$= \pi \left(\frac{32}{5} + \frac{16}{3} + 2\right)$$
$$= \pi \left(\frac{96 + 80 + 30}{15}\right) = \frac{206\pi}{15}$$
$$\boxed{V = \frac{206\pi}{15}}$$
Problem: Find the volume when the region between $y = x$ and $y = x^2$ is rotated around $y = 2$.
Step 1: Find intersection points
$x = x^2$ gives $x = 0$ and $x = 1$.
Step 2: Find outer and inner radii
Distance from $y = 2$:
- To $y = x^2$ (farther from $y = 2$): $R = 2 - x^2$
- To $y = x$ (closer to $y = 2$): $r = 2 - x$
Step 3: Set up and evaluate
$$V = \int_0^1 \pi \left[(2 - x^2)^2 - (2 - x)^2\right] dx$$
Expand:
- $(2 - x^2)^2 = 4 - 4x^2 + x^4$
- $(2 - x)^2 = 4 - 4x + x^2$
$$= \pi \int_0^1 (4 - 4x^2 + x^4 - 4 + 4x - x^2) \, dx$$
$$= \pi \int_0^1 (x^4 - 5x^2 + 4x) \, dx$$
$$= \pi \left[\frac{x^5}{5} - \frac{5x^3}{3} + 2x^2\right]_0^1$$
$$= \pi \left(\frac{1}{5} - \frac{5}{3} + 2\right)$$
$$= \pi \left(\frac{3 - 25 + 30}{15}\right) = \frac{8\pi}{15}$$
$$\boxed{V = \frac{8\pi}{15}}$$
Common Mistakes and Misunderstandings
❌ Mistake: Forgetting to square the radius
Wrong: $V = \int \pi f(x) \, dx$
Why it's wrong: The area of a circle is $\pi r^2$, not $\pi r$!
Correct: $V = \int \pi [f(x)]^2 \, dx$
❌ Mistake: Subtracting radii instead of squared radii
Wrong: $V = \int \pi [R(x) - r(x)]^2 \, dx$
Why it's wrong: Washer area is $\pi R^2 - \pi r^2$, NOT $\pi(R - r)^2$.
Correct: $V = \int \pi \left([R(x)]^2 - [r(x)]^2\right) dx$
❌ Mistake: Using the wrong radius for non-axis rotation
Wrong: Using $f(x)$ as radius when rotating around $y = k$.
Why it's wrong: The radius is the distance from the curve to the axis of rotation.
Correct: For rotation around $y = k$, radius = $|f(x) - k|$.
❌ Mistake: Confusing outer and inner radii
Wrong: Making the inner radius larger than the outer radius.
Why it's wrong: You'll get a negative volume, which is impossible!
Correct: The outer radius is the distance to the curve farther from the axis. Draw a picture and measure distances carefully.
Disk Method (Rotation about x-axis)
Volume when a region under y = f(x) is rotated around the x-axis. Each slice is a disk with radius f(x).
Variables:
- $V$:
- volume of the solid
- $f(x)$:
- the curve being rotated (radius of each disk)
- $a, b$:
- bounds on the x-axis
Washer Method
Volume when a region between two curves is rotated. Each slice is a washer (disk with hole). Outer minus inner, both squared.
Variables:
- $V$:
- volume of the solid
- $R(x)$:
- outer radius (farther curve from axis)
- $r(x)$:
- inner radius (closer curve to axis)
Disk Method (Rotation about y-axis)
Volume when a region is rotated around the y-axis. Express the curve as x = g(y) and integrate with respect to y.
Variables:
- $V$:
- volume of the solid
- $g(y)$:
- the curve as a function of y (radius of each disk)
- $c, d$:
- bounds on the y-axis
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.