Practice Final #2
Full CourseExam Settings
Short Answer Questions
Short AnswerFind the value of that makes continuous everywhere.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
For a piecewise function to be continuous at the transition point (in this case ), the limits from both sides must be equal:
The left-hand limit uses the first piece of the function:
The right-hand limit uses the second piece:
For continuity, these limits must be equal:
When working with piecewise functions, always check the value of each piece at the transition point to ensure continuity.
Therefore, the value of that makes continuous everywhere is:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We need to differentiate both sides of the equation with respect to :
Differentiating the left side:
Differentiating the right side:
At the point , we have and .
Let's substitute these values:
Now we need to calculate these values:
And:
Therefore:
We can simplify further:
Therefore:
When differentiating hyperbolic functions, remember that , similar to how the derivative of is for trigonometric functions.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We need to use the power rule for differentiation:
For the first term:
For the second term:
Now we combine these results to find :
When we substitute :
Therefore:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Evaluate the following limit:
Therefore:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
For the numerator:
For the denominator:
Therefore:
Long Answer Questions
Long AnswerExercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Let . Find the set on which the function is increasing.
When , , so:
When , , so:
Critical points occur when or when is undefined.
For :
This occurs when:
- , which is impossible for
- , which gives
For :
This occurs when:
- , which is impossible for
- , which gives , but this is outside our domain of
For :
Both formulations of the derivative approach 0 as approaches 0, so is also a critical point.
Therefore, our critical points are and .
For :
Since for , and for (because and ), we have for all .
For :
Since for , and for , we have for .
For :
Since for , and for , we have for .
Based on our analysis:
- For : (function is decreasing)
- For : (function is increasing)
- For : (function is decreasing)
- At and : (function is neither increasing nor decreasing)
Since we're looking for where the function is strictly increasing (not just non-decreasing), we exclude the critical points.
Therefore, the set on which is increasing is:
When finding intervals of increase/decrease, exclude critical points where the derivative equals zero, as the function is not strictly increasing or decreasing at those points.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Let and
Finding the derivatives:
Substituting into the quotient rule:
At :
The slope of the tangent line at is
Using the point-slope form of a line:
Let's find a point with a simple x-value, say :
Therefore, the point lies on the tangent line.
Find the value of for which .
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
For a constant , consider the plane region bounded by the curves and in the first quadrant.
The curves intersect when:
The solutions are and since:
- At : ✓
- At : ✓
For problems with intersecting curves, identify where they cross and determine which function has larger values in each subinterval to properly set up the volume integrals.
Let's compare and in the interval .
Both functions reach their maximum values at :
-
-
Since , the sine function is always above the parabola in the interval .
When rotating around the x-axis, we use the washer method where:
- Outer radius (sine function)
- Inner radius (parabola)
For the first term, using :
For the second term:
Therefore:
When rotating around the y-axis, we use the cylindrical shell method.
For each x from 0 to 1:
- Shell circumference = 2
- Shell height = (difference between the two curves)
- Shell thickness = dx
For the first term, using integration by parts:
For the second term:
For the third term:
Therefore:
We want:
The term appears on both sides, so we can divide by it:
Therefore:
Multi Part Questions
Multi-PartExercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
To find the equation of the tangent line to a function at a specific point , we use the **point-slope form** of a line:
Here, , and we need to find the tangent line at .
First, evaluate the function at :
Thus, the point on the curve is .
The derivative of is:
Now, evaluate the derivative at :
Thus, the slope of the tangent line at is .
Remember, the slope of the tangent line is the derivative evaluated at the given point.
We have the slope and the point . Using the point-slope form:
Simplify the equation:
Thus, the equation of the tangent line is:
The equation of the line tangent to at is:
This problem helps you practice finding the **equation of a tangent line** using the **point-slope formula**.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Sub-questions:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
From part (a), the equation of the tangent line to at was:
This equation gives us a linear approximation for around .
Linear approximations are most accurate near the point where the tangent line is calculated. Here, we use the tangent line to estimate .
1. **Substitute into the tangent line equation:**
2. **Simplify the expression:**
We start by rewriting the fractions with a common denominator. The least common denominator of and is 10:
Now simplify:
Thus, the linear approximation for is:
The linear approximation of based on the tangent line at is:
Linear approximations work best for values close to the point of tangency. Here, the approximation is most accurate for near .
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Sub-questions:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
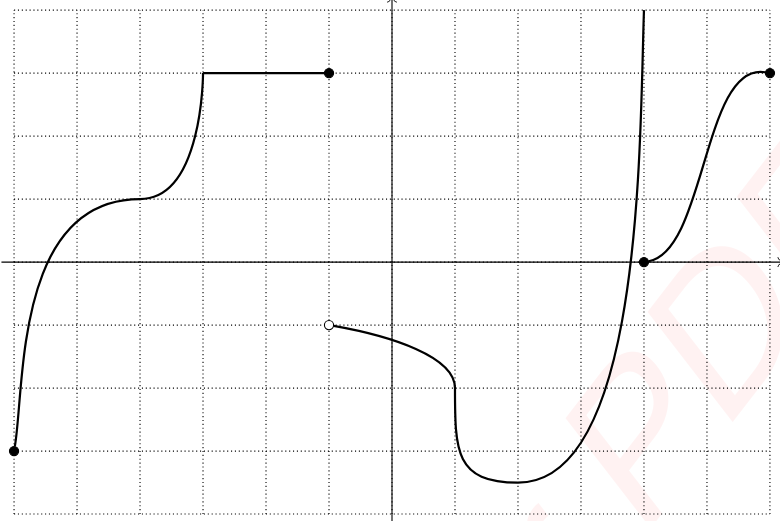
The first place to look is where . But this is just a derivative of 0, so that's totally fine.
Next we look at . This is a 'cusp' since it's a 'sharp turn' or 'corner'.
Any 'sharp turn' in a function are called a cusp and the derivative does not exist there.
So at we know the derivative does not exist.
Next we look at . Since the function is not even continuous there, we therefore also know that the function is not differentiable there.
So we add to our list.
The next point in question is when . Since it looks like the slope is completely vertical at , that makes the slope essentially infinite. That means the derivative does not exist there!
The derivative does not exist for any value where the function is totally vertical.
Moving on to the next point in question would be where . The function is not continuous there so therefore it is also not differentiable.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
which is the same as:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
From the graph we can see the slope is negative starting when and continues to be negative until .
There are two important exceptions when and when . The derivative does not exist at either of those points, so we can't include them in our final answer. Let's explain this:
When we have no left side limit, so the derivative does not exist.
When the derivative does not exist because the left hand limit and right hand limit both approach infinity.
So for our final answer we have only:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Another way to say it is this:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
NOTE: These points do not necessarily indicate an inflection point! For instance take the parabola when .
From the graph we can see an inflection point at together with a tangent line of finite slope (in this case the slope is 0), so the second derivative must be 0 there.
We also definitively have an inflection point when since the graph changes from concave up to concave down together with a tangent line. So for sure we have here at too.
We can't really tell what's happening when , but for this case the answer key will almost certainly not include this point. It's a local min which can indeed sometimes have (an example was given earlier with at ).
Careful with . Since the first derivative doesn't exist there, the second derivative can't exist either. So we have only at and .
Final solution is:
or just :
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
or just :
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
We can see a small concave up segment from when is between and .
Then it looks like another small segment when is between 1 and 4.
Then finally there is a small interval where is concave up right near then end when is between 4 and 5.
Note that x=4 is not included.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.