Practice Full Course (ID 17)
Full CourseExam Settings
Mcq Questions
MCQ(a) for all
(b) for all
(c) is decreasing and is increasing on
(d) for all
(e) for all
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Let . Let's check if it's even or odd.
Since , the integrand is an even function.
Consider . Let's use the substitution .
This means and .
We also change the limits of integration:
When , .
When , .
Substitute into the integral for :
Since is even, .
Using the property , we flip the limits and remove the negative sign from :
Now compare this to . Changing the variable of integration from to doesn't change the value.
Therefore, .
So, for all in the domain.
Based on the finding that :
(a) for all . This is TRUE.
(b) for all . Since , their derivatives must be equal: . Let's find using FTC Part 1: . So . The statement would imply , which is only true if . Thus, the statement is FALSE for .
(c) is decreasing and is increasing on . We found . Since and , both derivatives are non-negative (). Therefore, both functions are increasing (or non-decreasing). FALSE.
(d) for all . This implies . But . The integrand is strictly positive for . For , is the integral of a positive function over an interval of positive length, so . FALSE.
(e) for all . Since and we found for , this is FALSE.
The relationship between integrals of symmetric functions over symmetric limits is key. For an EVEN function , . For an ODD function , .
The only true statement is (a).
(a)
(b)
(c)
(d)
(e)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
A function is odd if for all .
A key property for definite integrals of odd functions is:
For any odd continuous function , for any in its domain.
We are asked to evaluate where .
We can split the interval of integration into two parts in a way that lets us use the property mentioned above. Since , we can split the integral at :
The first part of the split integral is .
Since is an odd function, we know that:
Substitute the result from Step 3 back into the split integral equation from Step 2:
This result matches option (c).
(a)
(b)
(c)
(d)
(e)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We need the area of the region bounded by the curve , the y-axis (which is the line ), and the horizontal line .
The curve passes through the origin .
The region is bounded on the left by , on the right by the curve, below by (where the curve meets the y-axis), and above by .
Since the region is defined by boundaries involving , it's convenient to integrate with respect to y.
We need to express the right boundary curve in the form .
Given , we cube both sides to solve for :
The left boundary is the y-axis, which has the equation .
When integrating with respect to y, the area between a right curve and a left curve from to is given by:
In our case:
The right curve is .
The left curve is .
The limits of integration are the y-values defining the region's vertical extent, which are from to .
So, the integral for the area is:
We evaluate the integral .
The antiderivative of is .
We evaluate this from to .
The result corresponds to option (d).
(a) the volume of a sphere of radius .
(b) the area of a circle of radius .
(c) the surface area of a sphere of radius .
(d) the volume of a cylinder of height and radius .
(e) the circumference of a circle of radius .
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
The expression appears inside the integral. Recall the equation of a circle centered at the origin with radius : . The upper semi-circle is given by .
The integral involves , which looks related to the disk method for finding volumes of revolution.
The volume of a solid generated by revolving the area under a curve from to around the x-axis is given by the disk method formula: .
Let's consider the function . If we revolve the area under this curve from to (which is a quarter-circle) around the x-axis, the volume generated is a hemisphere. Using the disk method, its volume would be:
The integral in the question is .
We can factor out the 2: .
Notice that is exactly the integral we identified as the volume of a hemisphere of radius .
Therefore, the given integral is .
Two hemispheres make a full sphere. So, the integral represents the volume of a sphere of radius .
We can directly calculate the integral to verify. The volume of a sphere is known to be . Let's see if the integral evaluates to this.
The calculation shows that the integral indeed equals the formula for the volume of a sphere. Therefore, the correct option is (a).
(a)
(b)
(c)
(d)
(e)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
The average value of a function over an interval is given by the integral of the function over that interval, divided by the length of the interval.
The formula for the average value of a function on the interval is:
For our specific function and the interval , we have and .
So, we need to calculate:
First, we find the antiderivative of . The integral of is .
Next, we evaluate the definite integral using the Fundamental Theorem of Calculus.
We evaluate the antiderivative at the upper limit () and subtract its value at the lower limit ().
Now we substitute the value of the integral back into the average value formula.
Remember that the length of the interval is .
Divide the result of the integral (which is 2) by the length of the interval () to get the average value.
True False Questions
True / FalseWhat is the rate of change when ?
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Using the product rule on the left side:
The derivative of the right side is:
Now apply the product rule to the left side:
This simplifies to:
First, isolate the term with :
Now, divide both sides by to get:
When , the expression becomes:
Thus, the rate of change when is:
The correct answer is:
Short Answer Questions
Short Answer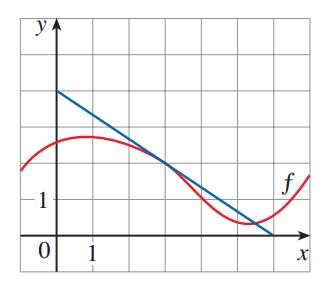
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
To evaluate , we first need to find the derivative of . We can rewrite this as . We must use the chain rule to find the derivative.
Next, we need to find two values from the provided graph: the value of the function and the slope of the tangent line at .
From the graph, we can see that the red curve passes through the point .
The blue line is the tangent line to the curve at . We can find its slope by identifying two points on the line, for example, and .
Now we substitute the values we found into the derivative formula from Step 1.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
First, notice that as , the expression inside the parentheses approaches 1, while the exponent approaches . This gives the indeterminate form , which often suggests that the limit involves the exponential function, . Our goal is to manipulate the expression to fit the standard form for the definition of . We can do this by rewriting the base, , into the form .
By rewriting as , we can split the fraction. This isolates a '1' which is crucial for the next step.
The key formula to remember is the limit definition of the exponential function: . Our entire strategy is to make our limit look like this form.
Now that our limit looks very similar to the definition, we can use a substitution to make it match perfectly.
Let . As , it's also true that . From this substitution, we also have . After substituting, we can split the exponent using the property . This allows us to separate the expression into two parts. The first part will match the definition of exactly, and the second part will be a simple limit to evaluate.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
The integrand is .
This function has an infinite discontinuity (a vertical asymptote) when the denominator is zero, i.e., when , which means .
Since this discontinuity occurs at the lower limit of integration, this is a Type 2 improper integral.
To evaluate this improper integral, we replace the problematic lower limit with a variable (say, ) and take the limit as approaches from the right side (since our interval is , we approach 1 from within the interval):
First, we find the antiderivative of .
Let , then .
So, .
Now, evaluate the definite integral from to :
Since , this simplifies to:
Since , is slightly greater than , so is a small positive number. Thus, .
So, the definite integral is .
Now we substitute this back into our limit expression:
Let . As , .
The limit becomes:
We know that .
Therefore:
When evaluating improper integrals with discontinuities, always rewrite them as a limit first. If the limit is , , or does not exist, the integral diverges. If the limit is a finite number, the integral converges to that number.
Since the limit is , the integral diverges.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
The expression in the denominator is a good candidate for substitution. Let's try substituting for the entire square root to simplify it.
Let .
Squaring both sides gives .
From this, we can express in terms of : .
Now, we need to find in terms of . Differentiate implicitly with respect to for the left side and for the right side (or solve for first: , then ).
Using implicit differentiation on :
.
We also need to express the numerator in terms of .
.
Alternatively, we can write the integral as . We already have and . This approach seems more direct.
A common strategy for integrals involving or similar expressions is to let be the entire square root, or the expression inside the square root. Letting simplifies the denominator directly to .
The integral is .
Substitute the expressions found in Step 1:
Numerator term .
Denominator .
Differential term .
So, the integral becomes:
The in the numerator and denominator cancels out (assuming , which is true if , i.e., ):
Now, find the antiderivative using the power rule for integration:
, where is the constant of integration.
Recall our substitution: .
Substitute this back into the expression for :
This is a correct answer, but it can be simplified by factoring out :
This is the simplified expression for the integral.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
The formula for integration by parts is .
We need to choose and . Using the LIATE (Logarithmic, Inverse trig, Algebraic, Trigonometric, Exponential) heuristic, we choose the algebraic part for .
Let and .
Then, we find and :
Now, apply the formula:
We now have a new integral, , which also requires integration by parts.
For the integral :
Let and .
Then, we find and :
Apply the formula to this part:
Now substitute the result from Step 2 back into the expression from Step 1:
We can group the terms with :
When performing integration by parts multiple times, keep track of your substitutions and be careful with signs. The LIATE heuristic (Logarithmic, Inverse Trig, Algebraic, Trig, Exponential) is a good guide for choosing .
Long Answer Questions
Long Answer(a) the x-axis
(b) the y-axis
Do not evaluate the integrals.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
First, we find the intersection points of and :
Set the -values equal:
This gives and .
When , . So, one intersection point is .
When , . So, the other intersection point is .
These will be our limits of integration in .
Next, determine which function is the "upper" function and which is the "lower" function in the interval .
Let's pick a test point, say :
For : .
For : .
Since , the line is above the parabola in the interval .
So, and .
For rotation about the x-axis, we can use the washer method.
The formula is .
Here, the outer radius is the distance from the x-axis to the upper curve , so .
The inner radius is the distance from the x-axis to the lower curve , so .
The limits of integration are from to .
The setup for the integral is:
For rotation about the y-axis, the cylindrical shells method is often more straightforward if our functions are already in the form .
The formula is .
Here, the radius of shell at a given is simply .
The height of shell at a given is .
The limits of integration are from to .
The setup for the integral is:
Alternatively, for part (b), you could use the washer method by integrating with respect to . This would require rewriting the functions as : and . Then and , with from 0 to 1. The integral would be . Both methods (shells wrt x, or washers wrt y) are valid for rotation about the y-axis.
(a) Rotation about the x-axis:
(b) Rotation about the y-axis (using cylindrical shells):
(Using washer method with respect to : )
(b) Rotation about the y-axis (using cylindrical shells):
(Using washer method with respect to : )
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
The first curve is already in this form: .
The second curve is . To express in terms of , we take the square root: .
Since implies , the relevant part of that can enclose an area with is (for ).
So, we are looking for the area between and .
To find the intersection points, we set the expressions for equal to each other:
Square both sides (note: ensure for to be real):
Factor out :
This gives or .
.
So, the curves intersect at and .
When , . Point: .
When , . Point: .
These are our limits of integration for .
In the interval , we need to determine which function has greater -values (the upper function) and which has smaller -values (the lower function).
Let's pick a test point within the interval, for example, .
For : .
For : .
Since , the function is the upper function, and is the lower function on the interval .
The area between two curves and from to is given by:
In our case, , , , and .
So, .
We can rewrite as .
Now, we find the antiderivative using the power rule for integration ():
So, the definite integral is:
Evaluate at the upper limit :
Evaluate at the lower limit :
Therefore, the area is:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
When rotating a region about the x-axis and integrating with respect to , the Method of Cylindrical Shells uses the formula:
Here:
- The integration is over the y-interval covering the region.
- The radius of a shell at height is .
- The height (or width) of the shell is the horizontal distance across the region at height , i.e., .
We need to rewrite the boundary curves and as functions of .
Line: .
Parabola: .
The right branch is .
The left branch is .
The intersection points found in Part A were and .
The lowest y-value in the region is .
The highest y-value is , the vertex of the parabola.
We need to consider the shell height across the range of y-values from 0 to 4.
- For between 0 and 3, the right boundary is the parabola () and the left boundary is the line (). Height .
- For between 3 and 4, the region is bounded by the parabola branches. The right boundary is and the left boundary is . Height .
Because the function defining the left boundary changes at , we must split the integral into two parts.
The y-limits are and , but we split at .
Substitute the expressions for and :
Both parts involve the integral . Let's find its antiderivative using u-substitution.
Let . Then and .
Substitute back :
Let .
First part:
We need and .
Second part:
We need .
The total volume is .
Note that this result, , matches the volume calculated using the Washer Method in Part A, as expected.
The volume of the solid obtained by rotating the region about the x-axis using the method of cylindrical shells is .
Word Problem Questions
Word ProblemExercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We are given the rate at which the radius is changing:
(The rate is negative because the radius is decreasing).
We need to find the rates at which the surface area and the volume are changing at the instant when the radius is cm.
That is, we need to find and when .
The formulas for the surface area and volume of a sphere with radius are:
Surface Area:
Volume:
Now, we differentiate both formulas with respect to time , using implicit differentiation because , , and are all functions of .
For Surface Area :
For Volume :
When performing implicit differentiation with respect to time , remember that differentiating a term involving requires multiplying by . For example, . Similarly, and .
Substitute cm and cm/hr into the equation for :
The surface area is decreasing at a rate of square centimeters per hour.
Substitute cm and cm/hr into the equation for :
The volume is decreasing at a rate of cubic centimeters per hour.
Notice that the formula for is . Since the surface area , we can also write . This sometimes provides a shortcut if the surface area is already known or easily calculated.
When the radius is 10 cm, the surface area is decreasing at a rate of cm²/hr and the volume is decreasing at a rate of cm³/hr.
When reaching and , the rate of change in the -direction is given by . What is at this point?
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
To find , we need to implicitly differentiate the equation with respect to , applying the chain rule to each term.
Starting with:
Differentiate each term with respect to :
**First term**:
**Second term**:
**Third term**:
Using the product rule:
Now, combine all terms:
Group the terms:
Substitute , , and :
Simplify each term:
Solve for :
Multi Part Questions
Multi-PartExercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Sub-questions:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We want to divide by .
The initial setup is:
___________
x^2+2 | x^3 + 5x^2 - 2x + 1
1. First term of quotient: Divide the leading term of the dividend () by the leading term of the divisor (): . Write in the quotient area.
x
___________
x^2+2 | x^3 + 5x^2 - 2x + 1
2. First multiplication: Multiply the term by the entire divisor (): . Write this result below the dividend, aligning terms by power.
x
___________
x^2+2 | x^3 + 5x^2 - 2x + 1
x^3 + 2x
3. First subtraction: Subtract the result from the dividend. Draw a line and write the result below. Remember to subtract corresponding terms: , , . Bring down the next term () from the dividend.
x
___________
x^2+2 | x^3 + 5x^2 - 2x + 1
-(x^3 + 2x)
________________
5x^2 - 4x + 1
4. Second term of quotient: Divide the leading term of the new remainder () by the leading term of the divisor (): . Write in the quotient area.
x + 5
___________
x^2+2 | x^3 + 5x^2 - 2x + 1
-(x^3 + 2x)
________________
5x^2 - 4x + 1
5. Second multiplication: Multiply the term by the divisor (): . Write this result below the current remainder, aligning terms.
x + 5
___________
x^2+2 | x^3 + 5x^2 - 2x + 1
-(x^3 + 2x)
________________
5x^2 - 4x + 1
5x^2 + 10
6. Second subtraction: Subtract the result from . Draw a line and write the final result. , , . The result is .
x + 5 <-- Quotient s(x)
___________
x^2+2 | x^3 + 5x^2 - 2x + 1
-(x^3 + 2x)
________________
5x^2 - 4x + 1
-(5x^2 + 10)
____________
-4x - 9 <-- Remainder r(x)
The degree of this result (, degree 1) is less than the degree of the divisor (, degree 2), so the algorithm stops.
Double-check each subtraction step carefully, especially handling signs and aligning terms correctly (like the under and under ).
From the final division layout:
The quotient is .
The remainder is .
The degree of is 1, which is less than the degree of the divisor (). The condition is satisfied.
The result is: .
Using polynomial long division, we found the quotient and the remainder . The degree of is 1, which is less than 2.
So, .
Using polynomial long division, we found the quotient and the remainder . The degree of is 1, which is less than 2.
So, .
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Using the quotient and remainder found previously, we rewrite the integrand:
We can split this into the sum of two integrals:
The first integral is a simple polynomial integration:
The second integral involves the proper rational function . Since the denominator is an irreducible quadratic, we split the fraction based on the derivative of the denominator and a constant term. The derivative of is .
This split is strategic: the first part () can be solved with a u-substitution for the denominator, leading to a logarithm. The second part () matches the arctangent integration form.
Use u-substitution. Let . Then , which means .
(Absolute value is dropped since is always positive).
Therefore, the first part of the rational integral evaluates to .
This matches the arctangent integration formula .
Here, and , so .
Therefore, the second part of the rational integral evaluates to .
Combine the results from Step 2, Step 3a, and Step 3b. Don't forget a single constant of integration at the end. The integral is:
The integral evaluates to:
The integral evaluates to:
is given.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Sub-questions:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We start with the implicit equation:
Differentiate both sides with respect to . For terms involving , we will use the chain rule because is a function of .
**First term**:
Using the chain rule:
**Second term**:
Using the product rule:
**Third term**:
Now, putting everything together:
Distribute the :
Now group terms involving :
Solve for :
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
From part (a), we found the derivative of the curve to be:
We need to find the slope of the tangent line at .
Substitute and into the derivative:
Simplify:
Thus, the slope of the tangent line at is .
The point-slope form of the equation of a line is:
Substitute the point and the slope :
Simplify:
Now, expand the equation:
Add 1 to both sides to solve for :
Simplify:
Thus, the equation of the tangent line is: