Domain and Range for MATH 122
Exam Relevance for MATH 122
Prerequisite review. Not tested directly in MATH 122.
This skill appears on:
What is Domain and Range?
Every function is like a machine: you put something in (the input), and you get something out (the output). But not every machine accepts every input — and not every output is possible.
- Domain = all the valid inputs (x-values) you can plug into the function
- Range = all the possible outputs (y-values) the function can produce
Understanding domain and range helps you know where a function "lives" — which values make sense to use and which results you can expect.
Visualizing Domain and Range
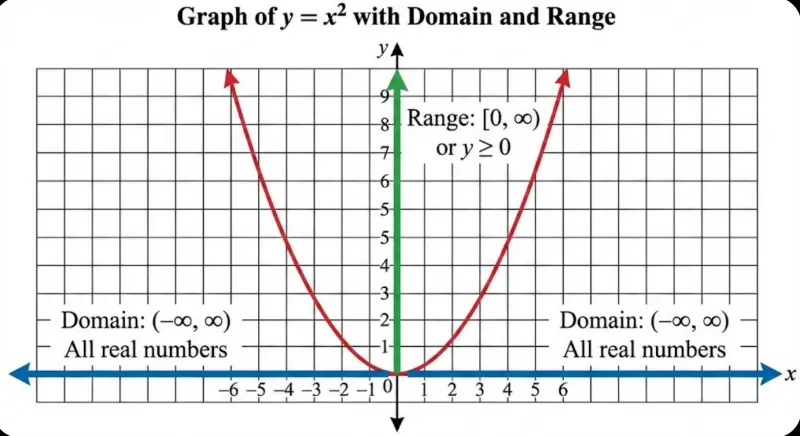
In this graph, notice that:
- Domain: You can plug in ANY x-value (the parabola extends left and right forever) → Domain: $(-\infty, \infty)$
- Range: The outputs only go from 0 upward (the parabola never dips below the x-axis) → Range: $[0, \infty)$
Interval Notation Quick Reference
| Notation | Meaning | When to Use |
|---|---|---|
| $(a, b)$ | All numbers between $a$ and $b$, not including $a$ or $b$ | Open interval |
| $[a, b]$ | All numbers between $a$ and $b$, including $a$ and $b$ | Closed interval |
| $[a, b)$ | Includes $a$, excludes $b$ | Half-open |
| $(-\infty, a)$ | All numbers less than $a$ | Unbounded left |
| $(a, \infty)$ | All numbers greater than $a$ | Unbounded right |
| $(-\infty, \infty)$ | All real numbers | No restrictions |
💡 Key rule: Always use parentheses with $\infty$ or $-\infty$ — you can never "reach" infinity, so you can't include it!
Finding the Domain
The domain is usually "all real numbers" except where the function breaks. Look for these common restrictions:
Restriction 1: Division by Zero
You cannot divide by zero. If the function has a denominator, set it $\neq 0$.
$$f(x) = \frac{1}{x-3}$$
The denominator is $x - 3$. Set it $\neq 0$:
$$x - 3 \neq 0 \implies x \neq 3$$
Domain: $(-\infty, 3) \cup (3, \infty)$ — all real numbers except 3.
Restriction 2: Square Roots of Negatives
You cannot take the square root of a negative number (in real numbers). The expression under the root must be $\geq 0$.
$$g(x) = \sqrt{x + 2}$$
Set the inside $\geq 0$:
$$x + 2 \geq 0 \implies x \geq -2$$
Domain: $[-2, \infty)$
Restriction 3: Logarithms of Non-Positives
You cannot take the logarithm of zero or a negative number. The input to a log must be $> 0$.
$$h(x) = \ln(x - 5)$$
Set the inside $> 0$:
$$x - 5 > 0 \implies x > 5$$
Domain: $(5, \infty)$
Combining Restrictions
Some functions have multiple restrictions. Find each one, then combine.
$$f(x) = \frac{\sqrt{x}}{x - 4}$$
- Square root: $x \geq 0$
- Denominator: $x \neq 4$
Domain: $[0, 4) \cup (4, \infty)$
Finding the Range
The range is often trickier than the domain. Here are strategies:
Strategy 1: Use the Graph
For $f(x) = \frac{1}{x}$:
- The graph approaches but never touches $y = 0$
- The function produces every other y-value
- Range: $(-\infty, 0) \cup (0, \infty)$ — all real numbers except 0
Strategy 2: Think About What Outputs Are Possible
For $f(x) = x^2$:
- Squaring any number gives a non-negative result
- You can get 0 (when $x = 0$)
- You can get arbitrarily large values (as $x \to \pm\infty$)
- Range: $[0, \infty)$
Strategy 3: Solve for x in Terms of y
Set $y = f(x)$ and solve for $x$. The values of $y$ that give valid solutions are in the range.
For $f(x) = 2x + 1$:
$$y = 2x + 1$$ $$y - 1 = 2x$$ $$x = \frac{y - 1}{2}$$
This gives a valid $x$ for ANY value of $y$. Range: $(-\infty, \infty)$
Find the domain and range of $f(x) = \sqrt{9 - x^2}$.
Step 1: Find the domain
The expression under the square root must be $\geq 0$:
$$9 - x^2 \geq 0$$ $$9 \geq x^2$$ $$-3 \leq x \leq 3$$
Domain: $[-3, 3]$
Step 2: Find the range
- The minimum value of $\sqrt{9 - x^2}$ is $0$ (when $x = \pm 3$)
- The maximum value is $\sqrt{9} = 3$ (when $x = 0$)
Range: $[0, 3]$
Step 3: Visualize
This is actually the top half of a circle with radius 3!
Find the domain and range of $f(x) = \frac{x + 1}{x - 2}$.
Step 1: Find the domain
Denominator $\neq 0$:
$$x - 2 \neq 0 \implies x \neq 2$$
Domain: $(-\infty, 2) \cup (2, \infty)$
Step 2: Find the range
Solve for $x$:
$$y = \frac{x + 1}{x - 2}$$
$$y(x - 2) = x + 1$$
$$yx - 2y = x + 1$$
$$yx - x = 2y + 1$$
$$x(y - 1) = 2y + 1$$
$$x = \frac{2y + 1}{y - 1}$$
This is undefined when $y = 1$. So $y = 1$ is NOT in the range.
Range: $(-\infty, 1) \cup (1, \infty)$
Using the graph below, find the domain and range of the piecewise function.
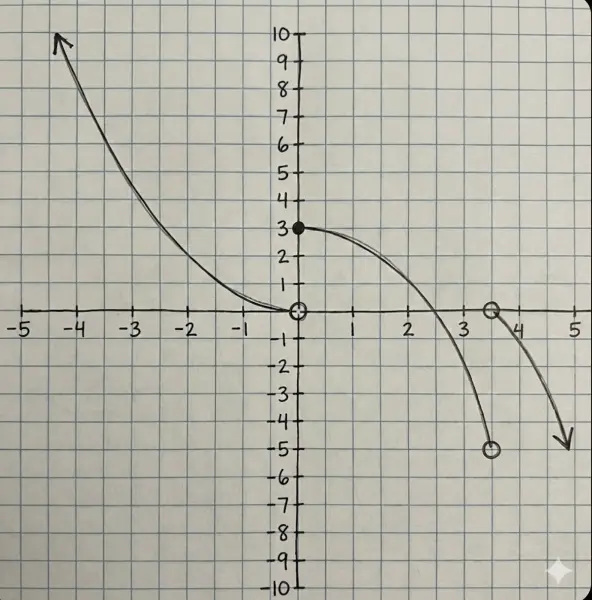
When reading domain and range from a graph:
- Domain: Look at how far left and right the graph extends (x-axis coverage)
- Range: Look at how far up and down the graph extends (y-axis coverage)
- Closed dots (●) mean the point IS included — use a bracket $[$
- Open dots (○) mean the point is NOT included — use a parenthesis $($
Finding the Domain:
- The first piece extends from the upper left (toward $x = -\infty$) and ends at $x = 0$ with an open circle
- The second piece starts at $x = 0$ with a closed dot and ends at $x = 3.5$ with an open circle
- The third piece starts at $x = 3.5$ with an open circle and extends to the lower right (toward $x = +\infty$)
At $x = 0$: The closed dot means $x = 0$ IS included.
At $x = 3.5$: Both adjacent pieces have open circles, so $x = 3.5$ is NOT included.
$$\boxed{\text{Domain: } (-\infty, 3.5) \cup (3.5, \infty)}$$
Finding the Range:
- The first piece has an arrow pointing up toward $+\infty$
- The third piece has an arrow pointing down toward $-\infty$
- Together, every y-value from $-\infty$ to $+\infty$ is covered
$$\boxed{\text{Range: } (-\infty, \infty)}$$
Common Mistakes and Misunderstandings
❌ Mistake: Using brackets with infinity
Wrong: $[0, \infty]$
Why it's wrong: Infinity is not a number — you can never "reach" it. You can't include something that doesn't exist as a specific value.
Correct: $[0, \infty)$
❌ Mistake: Forgetting to check ALL restrictions
Wrong: For $f(x) = \frac{\sqrt{x}}{x-1}$, saying domain is $x \neq 1$
Why it's wrong: You found the denominator restriction but forgot the square root restriction ($x \geq 0$).
Correct: Domain: $[0, 1) \cup (1, \infty)$
❌ Mistake: Confusing domain and range
Wrong: "The range of $f(x) = x^2$ is all real numbers because you can plug in any x."
Why it's wrong: That describes the domain, not the range. The range asks what outputs are possible.
Correct: Domain: $(-\infty, \infty)$. Range: $[0, \infty)$ because $x^2$ is never negative.
Domain
The set of all valid input values (x-values) for which the function produces a real output.
Variables:
- $x$:
- input value
- $f(x)$:
- the function
Range
The set of all possible output values (y-values) that the function can produce.
Variables:
- $y$:
- output value
- $f(x)$:
- the function
- $x$:
- input from the domain
Square Root Domain Restriction
For real numbers, you cannot take the square root of a negative. Set the expression under the root ≥ 0 and solve.
Variables:
- $\text{expression}$:
- whatever is under the square root
Denominator Restriction
Division by zero is undefined. Set the denominator ≠ 0 and solve to find excluded values.
Variables:
- $\text{denominator}$:
- the bottom of the fraction
Logarithm Domain Restriction
Logarithms are only defined for positive inputs. Set the expression inside the log > 0 and solve.
Variables:
- $\text{expression}$:
- the input to the logarithm
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.