Practice Final #6
Full CourseExam Settings
Short Answer Questions
Short AnswerExercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Always check for symmetry properties first when evaluating definite integrals over intervals like [-a,a]. This can save significant calculation time.
Let's examine if the integrand has symmetry properties:
- is even (same value for and )
- will have the same value at and since is even
- is odd (changes sign when changes to )
Therefore, is an odd function because an even function multiplied by an odd function results in another odd function:
For any odd function , the definite integral over a symmetric interval is always zero:
Since our integrand is odd and the interval is symmetric about the origin, we can immediately conclude:
This problem tests your ability to:
1. Recognize and apply symmetry properties of functions
2. Understand how odd functions behave when integrated over symmetric intervals
The professor included this problem to teach you to always look for structural properties and symmetry before attempting more complicated integration techniques. Recognizing oddness/evenness can save significant time and effort in many calculus problems.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We need to find the area of one complete positive region bounded by:
- The curve
- The x-axis where
At the x-axis, :
This occurs at for integer values of .
Since we want one complete positive region, we need to identify where the function is positive. The cosine function is positive in the interval for integer values of .
For simplicity, let's choose the interval , which contains one complete positive region.
In the interval , the cosine function is positive, with its maximum value of 1 at . This means our function is non-negative throughout the interval and reaches a maximum value of 2 at .
For a region bounded by , the x-axis, , and , the area is
For our problem:
Therefore:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We need to find the derivative of a function defined by a definite integral with a variable upper limit.
Using the Fundamental Theorem of Calculus:
If , then
In our case:
- (the upper limit of integration)
- (the integrand)
- (the derivative of the upper limit)
Therefore:
Your professor designed this problem to test your understanding of the Fundamental Theorem of Calculus with variable limits.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
To evaluate this limit, start by simplifying the expression within the tangent function. We’ll try factoring the numerator and the denominator.
The numerator can be factored by grouping terms.
To factor , we group the terms in pairs:
Now, factor out from the first group and factor out from the second group:
Now we have a common factor of :
The denominator factors as:
So, the expression becomes:
Now, cancel the common factor from both the numerator and the denominator:
Now that we’ve simplified the expression, we can substitute directly:
Tip: You need to know the unit circle and the values of common trigonometric functions at special angles, such as , to solve problems like this.
Since , we have:
This question is designed to test your ability to handle limits involving trigonometric functions, especially by simplifying rational expressions through factoring. The professor likely included this question to emphasize the importance of **factoring and cancelling terms** before evaluating limits, a common approach in calculus to avoid indeterminate forms.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
To differentiate , we use the quotient rule, which states:
Quotient Rule: If , then
In this case:
-
-
**Derivative of** :
**Derivative of** :
Now, substitute , , , and into the quotient rule formula:
Distribute and :
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Long Answer Questions
Long AnswerExercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
For the integral
you need to identify where the integrand becomes improper.
The denominator
equals zero when , which is the upper limit of integration. This makes the integral improper since the integrand becomes unbounded at .
When evaluating improper integrals, check if the integrand becomes unbounded at any point in the interval of integration, including the endpoints.
To handle the improper behavior at , rewrite the integral as a limit:
First, find the indefinite integral:
Use substitution with , so or :
Apply the power rule:
Now evaluate using the limits:
As approaches , the term
approaches infinity:
Therefore:
Since the limit diverges to infinity, the improper integral diverges:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We need to find the area between the curves and over the interval .
First, let's evaluate these functions at the endpoints:
At :
At :
Let's find where :
Since , we have:
This occurs when , which happens at .
Based on our analysis:
- For :
- For :
When finding area between curves that cross, split the integral at intersection points and use absolute value of the difference in each region.
Using the tip: the area is calculated as:
When working with expressions like or , always try to apply the double angle formula to simplify integration.
We can simplify using the identity :
Therefore:
This problem tests your ability to:
1. Recognize trigonometric identities that simplify the calculation
2. Find intersection points of curves algebraically
3. Set up integrals correctly based on where one curve is above the other
4. Use the double-angle formula for cosine to simplify integration
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
For the natural logarithm , the argument must be greater than zero. In this case that means:
which is therefore our first condition that we need to satisfy.
The function is defined for all because for all real values of .
So there are no added restrictions on the domain from .
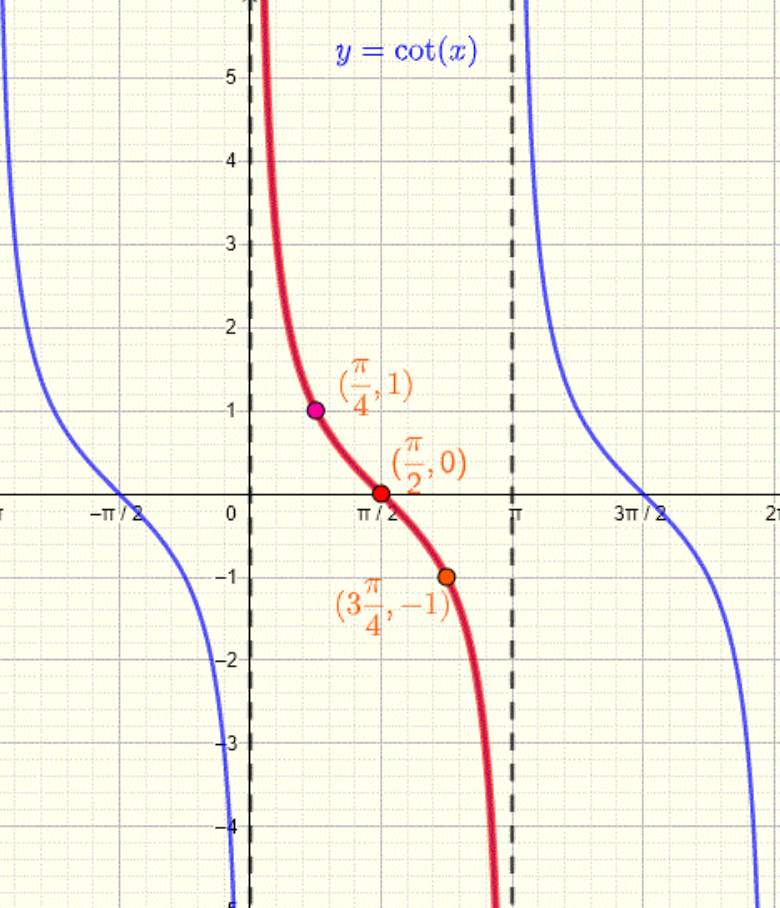
Figure: graph of cotangent
You also will need to know the unit circle values.
To satisfy the condition for the logarithm, we need:
This simplifies to:
Now, we find the values of such that .
Since decreases as increases, we need:
From the unit circle, we know , so:
Taking the square root of both sides:
Thus, the domain of the function is:
This problem tests your understanding of the domain of composite functions, especially when involving inverse trigonometric functions and logarithms. The professor likely included this question to ensure you know how to work with domain restrictions and analyze inequalities involving inverse trigonometric expressions.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.