Transformations for MATH 122
Exam Relevance for MATH 122
Prerequisite review. Function transformations not tested directly.
Understanding Function Transformations
When you learn a "parent function" like $f(x) = x^2$, you can create infinitely many related functions by shifting, stretching, or flipping it. These modifications are called transformations.
Instead of memorizing the shape of every function, you can start with a basic shape and transform it. This makes graphing much faster and helps you understand how equations relate to their graphs.
The Four Main Transformations
| Transformation | What it does | Equation form |
|---|---|---|
| Vertical shift | Moves graph up or down | $f(x) + k$ |
| Horizontal shift | Moves graph left or right | $f(x - h)$ |
| Vertical stretch/compress | Makes graph taller or shorter | $a \cdot f(x)$ |
| Reflection | Flips graph across an axis | $-f(x)$ or $f(-x)$ |
Vertical Shifts: $f(x) + k$
Adding a constant outside the function shifts the graph vertically.
- $f(x) + k$ shifts up by $k$ units (when $k > 0$)
- $f(x) - k$ shifts down by $k$ units
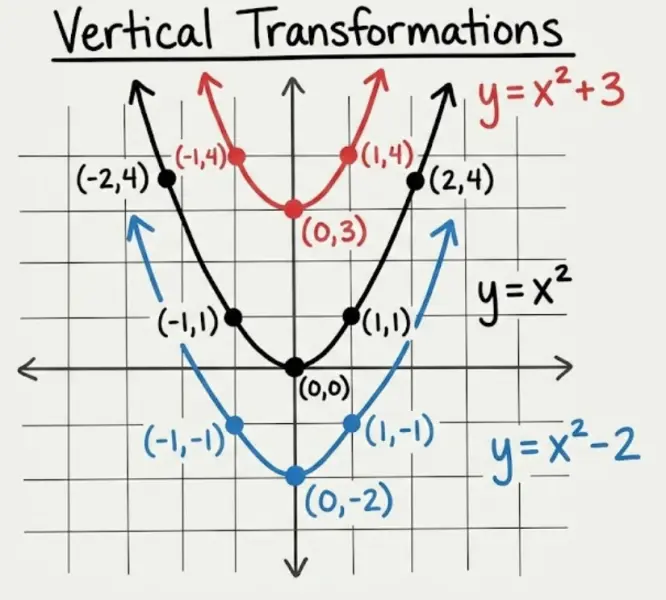
Notice how the shape stays exactly the same — only the position changes. The vertex of $x^2$ moves from $(0,0)$ to $(0,3)$ or $(0,-2)$.
Horizontal Shifts: $f(x - h)$
Adding a constant inside the function (to $x$) shifts the graph horizontally.
⚠️ This one is counterintuitive! The shift is opposite to what you might expect.
- $f(x - h)$ shifts right by $h$ units (when $h > 0$)
- $f(x + h)$ shifts left by $h$ units
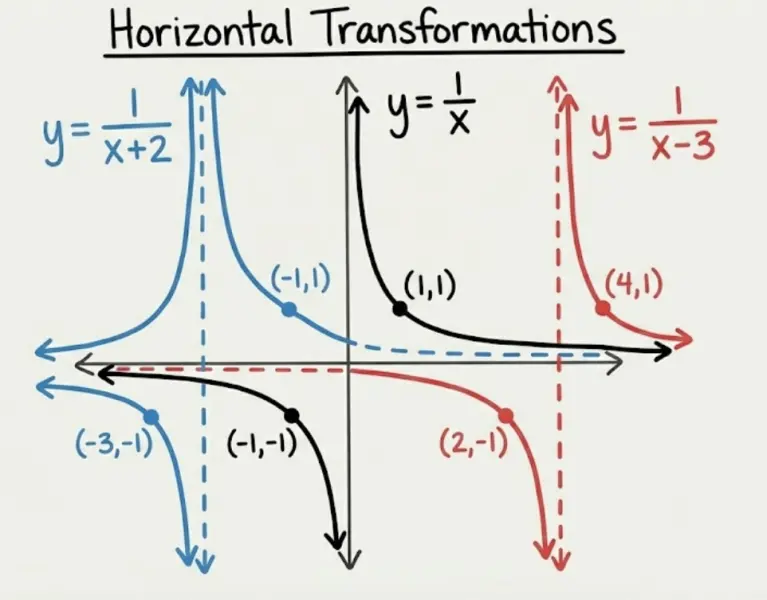
Why is it backwards? Think about it: $\frac{1}{x+2}$ has its vertical asymptote where $x + 2 = 0$, which is $x = -2$. So adding 2 inside shifts left. Similarly, $\frac{1}{x-3}$ shifts right to $x = 3$.
Vertical Stretch and Compression: $a \cdot f(x)$
Multiplying the function by a constant $a$ stretches or compresses it vertically.
- $|a| > 1$: Stretch (taller)
- $0 < |a| < 1$: Compression (shorter)
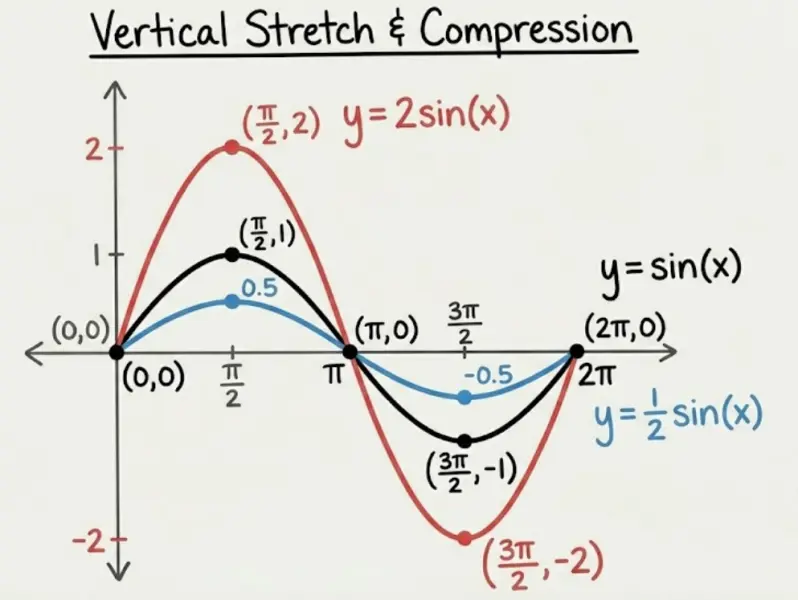
Notice how $\sin(x)$ normally oscillates between $-1$ and $1$. With $2\sin(x)$, the amplitude doubles (oscillates between $-2$ and $2$). With $\frac{1}{2}\sin(x)$, the amplitude is halved.
Reflections
Reflection across the x-axis: $-f(x)$
Negating the output flips the graph upside down (over the x-axis).
Reflection across the y-axis: $f(-x)$
Negating the input flips the graph horizontally (mirror image over the y-axis).
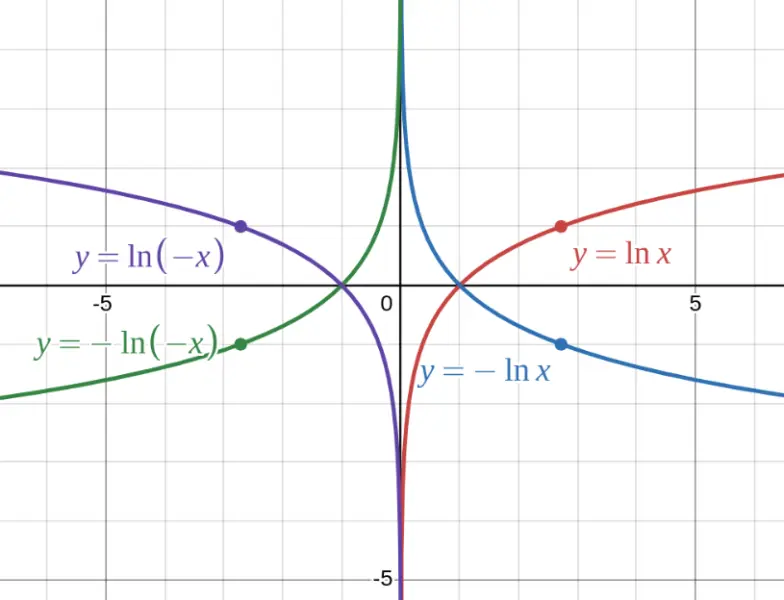
Starting with $\ln(x)$ (defined for $x > 0$):
- $\ln(-x)$ reflects over the y-axis (now defined for $x < 0$)
- $-\ln(x)$ reflects over the x-axis (flipped upside down)
- $-\ln(-x)$ reflects over both axes (rotated 180°)
Describe the transformations applied to $f(x) = x^2$ to get $g(x) = -(x-2)^2 + 5$.
Starting with $f(x) = x^2$, we apply:
- Horizontal shift right 2: $(x-2)^2$
- Reflection over x-axis: $-(x-2)^2$
- Vertical shift up 5: $-(x-2)^2 + 5$
The vertex moves from $(0,0)$ to $(2, 5)$, and the parabola opens downward.
The graph of $f(x) = |x|$ is shifted left 4 units, stretched vertically by a factor of 3, and shifted down 1 unit. Write the equation.
Apply transformations in order:
- Shift left 4: $|x + 4|$
- Vertical stretch by 3: $3|x + 4|$
- Shift down 1: $3|x + 4| - 1$
$$\boxed{g(x) = 3|x + 4| - 1}$$
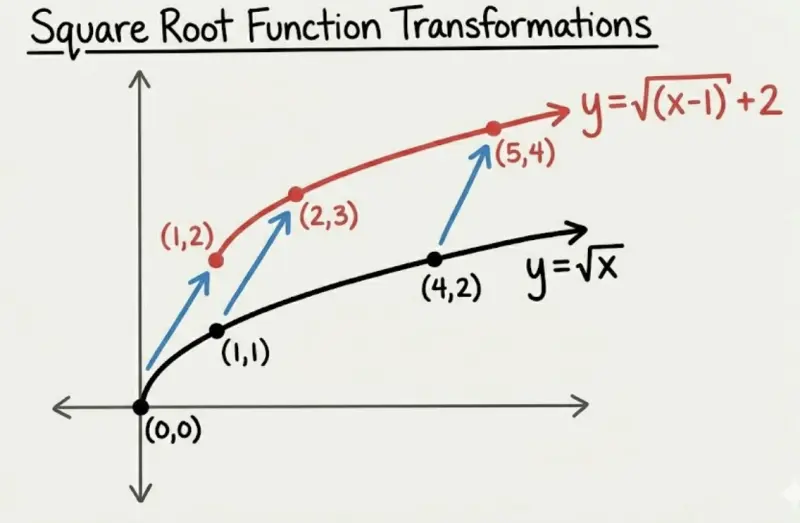
Sketch $g(x) = f(x+1) + 2$ by transforming $f(x) = \sqrt{x}$.
Starting from $f(x) = \sqrt{x}$:
- Shift right 1: The starting point moves from $(0, 0)$ to $(1, 0)$
- Shift up 2: The starting point moves from $(1, 0)$ to $(1, 2)$
Key points on $f(x) = \sqrt{x}$: $(0,0)$, $(1,1)$, $(4,2)$
After transformation: $(1, 2)$, $(2, 3)$, $(5, 4)$
Order of Transformations
When multiple transformations are combined, apply them in this order:
- Horizontal shifts (inside the function)
- Horizontal stretches/reflections (inside the function)
- Vertical stretches/reflections (outside the function)
- Vertical shifts (outside the function)
Memory trick: Work from the inside out — transformations closer to $x$ happen first.
The General Form
$$g(x) = a \cdot f(b(x - h)) + k$$
| Parameter | Effect |
|---|---|
| $a$ | Vertical stretch ($\|a\| > 1$) or compression ($0 < \|a\| < 1$); negative = flip over x-axis |
| $b$ | Horizontal stretch ($0 < \|b\| < 1$) or compression ($\|b\| > 1$); negative = flip over y-axis |
| $h$ | Horizontal shift (right if $h > 0$, left if $h < 0$) |
| $k$ | Vertical shift (up if $k > 0$, down if $k < 0$) |
Common Mistakes and Misunderstandings
❌ Mistake: Getting horizontal shifts backwards
Wrong: $f(x - 3)$ shifts left 3 units
Why it's wrong: The shift is opposite to the sign inside. Think: "What value of $x$ makes the inside equal zero?"
Correct: $f(x - 3)$ shifts right 3 units. $f(x + 3)$ shifts left.
❌ Mistake: Confusing stretch direction
Wrong: $2f(x)$ makes the graph wider
Why it's wrong: Multiplying by 2 makes every y-value twice as large, so the graph gets taller (narrower for parabolas).
Correct: $2f(x)$ is a vertical stretch — the graph gets taller/narrower. $\frac{1}{2}f(x)$ compresses it.
❌ Mistake: Applying transformations in the wrong order
Wrong: For $2(x-3)^2 + 1$, shifting up 1 first, then shifting right 3
Why it's wrong: You must follow the correct order: horizontal shifts, then stretches, then vertical shifts.
Correct: Shift right 3, then stretch by 2, then shift up 1.
Vertical Shift
Shifts the graph up (k > 0) or down (k < 0) by k units. The shape stays the same.
Variables:
- $k$:
- vertical shift amount (positive = up, negative = down)
- $f(x)$:
- the original function
Horizontal Shift
Shifts the graph right (h > 0) or left (h < 0) by h units. Note: the shift is OPPOSITE to the sign!
Variables:
- $h$:
- horizontal shift amount (positive = right, negative = left)
- $f(x)$:
- the original function
Vertical Stretch/Compression
Stretches (|a| > 1) or compresses (0 < |a| < 1) the graph vertically. If a < 0, also reflects over the x-axis.
Variables:
- $a$:
- stretch factor (|a| > 1 = taller, 0 < |a| < 1 = shorter)
- $f(x)$:
- the original function
General Transformation Form
The complete transformation formula combining all four types: stretch, compression, shifts, and reflections.
Variables:
- $a$:
- vertical stretch/compression and x-axis reflection
- $b$:
- horizontal stretch/compression and y-axis reflection
- $h$:
- horizontal shift (opposite sign!)
- $k$:
- vertical shift
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.