Area Between Curves for MATH 122
Exam Relevance for MATH 122
Common application problem. Setting up and evaluating integrals for area.
This skill appears on:
Understanding Area Between Curves
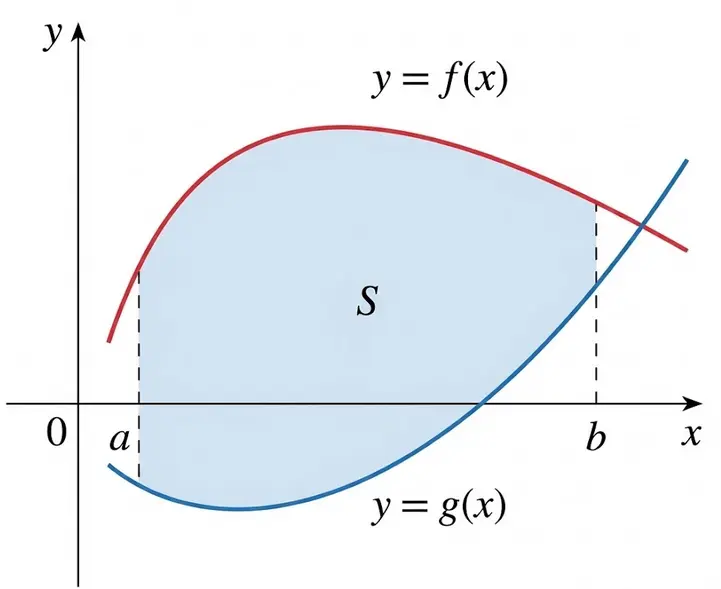
You already know how to find the area under a single curve using integration. But what if you want to find the area between two curves? This comes up constantly — finding the area of a region bounded by multiple functions.
The key idea: Area between curves = (top curve) − (bottom curve), integrated over the region.
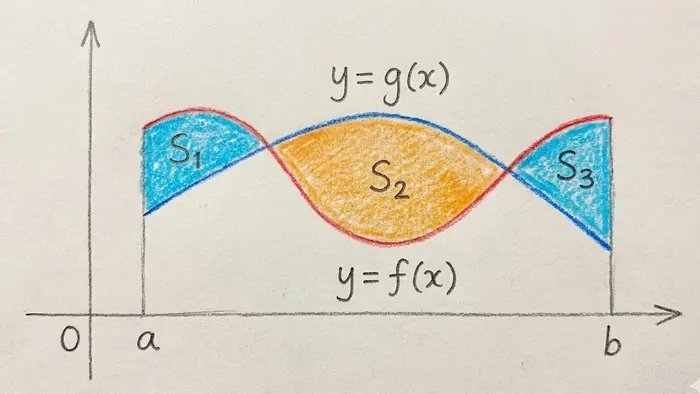
If there are multiple intersection points and changes in which function is 'on top', you add up the individual regions! Do not subtract them:
The Basic Formula
For two functions where $f(x) \geq g(x)$ on $[a, b]$:
$$A = \int_a^b [f(x) - g(x)] \, dx$$
In words: top minus bottom, integrated from left to right.
Key Steps
- Sketch the region (even a rough sketch helps!)
- Find intersection points (solve $f(x) = g(x)$) — these are often your limits
- Identify which curve is on top in each interval
- Set up the integral: $\int (\text{top} - \text{bottom}) \, dx$
- Evaluate
Problem: Find the area of the region bounded by $y = x^2$ and $y = x + 2$.
Step 1: Find intersection points
Set $x^2 = x + 2$:
$$x^2 - x - 2 = 0$$
$$(x-2)(x+1) = 0$$
$$x = -1, \quad x = 2$$
Step 2: Determine which is on top
At $x = 0$: $y = 0^2 = 0$ and $y = 0 + 2 = 2$
The line $y = x + 2$ is on top.
Step 3: Set up and evaluate
$$A = \int_{-1}^{2} [(x + 2) - x^2] \, dx$$
$$= \int_{-1}^{2} (x + 2 - x^2) \, dx$$
$$= \left[\frac{x^2}{2} + 2x - \frac{x^3}{3}\right]_{-1}^{2}$$
At $x = 2$: $2 + 4 - \frac{8}{3} = 6 - \frac{8}{3} = \frac{10}{3}$
At $x = -1$: $\frac{1}{2} - 2 + \frac{1}{3} = -\frac{7}{6}$
$$A = \frac{10}{3} - \left(-\frac{7}{6}\right) = \frac{10}{3} + \frac{7}{6} = \frac{27}{6} = \frac{9}{2}$$
$$\boxed{A = \frac{9}{2} = 4.5}$$
Problem: Find the area enclosed by $y = x^2$ and $y = 2x - x^2$.
Step 1: Find intersection points
$$x^2 = 2x - x^2$$
$$2x^2 - 2x = 0$$
$$2x(x - 1) = 0$$
$$x = 0, \quad x = 1$$
Step 2: Determine which is on top
At $x = 0.5$:
- $y = (0.5)^2 = 0.25$
- $y = 2(0.5) - (0.5)^2 = 1 - 0.25 = 0.75$
The curve $y = 2x - x^2$ is on top.
Step 3: Set up and evaluate
$$A = \int_0^1 [(2x - x^2) - x^2] \, dx$$
$$= \int_0^1 (2x - 2x^2) \, dx$$
$$= \left[x^2 - \frac{2x^3}{3}\right]_0^1$$
$$= 1 - \frac{2}{3} = \frac{1}{3}$$
$$\boxed{A = \frac{1}{3}}$$
Problem: Find the area between $y = x^3$ and $y = x$.
Step 1: Find intersection points
$$x^3 = x$$
$$x^3 - x = 0$$
$$x(x^2 - 1) = 0$$
$$x = -1, \quad x = 0, \quad x = 1$$
Step 2: Determine which is on top in each region
On $[-1, 0]$: At $x = -0.5$, $y = (-0.5)^3 = -0.125$ and $y = -0.5$
So $x^3 > x$ (cubic is on top).
On $[0, 1]$: At $x = 0.5$, $y = 0.125$ and $y = 0.5$
So $x > x^3$ (line is on top).
Step 3: Set up two integrals
$$A = \int_{-1}^{0} (x^3 - x) \, dx + \int_0^1 (x - x^3) \, dx$$
First integral: $$\left[\frac{x^4}{4} - \frac{x^2}{2}\right]_{-1}^{0} = 0 - \left(\frac{1}{4} - \frac{1}{2}\right) = \frac{1}{4}$$
Second integral: $$\left[\frac{x^2}{2} - \frac{x^4}{4}\right]_0^1 = \frac{1}{2} - \frac{1}{4} = \frac{1}{4}$$
$$\boxed{A = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}}$$
Integrating with Respect to y
Sometimes it's easier to integrate horizontally (with respect to $y$).
$$A = \int_c^d [\text{right} - \text{left}] \, dy$$
Use this when:
- The region is easier to describe using $y$-bounds
- Curves are given as $x = g(y)$
- Integrating with respect to $x$ would require multiple integrals
Problem: Find the area bounded by $y = x - 1$ and $y^2 = 2x + 6$.
Step 1: Rewrite curves as x = g(y)
From $y = x - 1$: $x = y + 1$
From $y^2 = 2x + 6$: $x = \frac{y^2 - 6}{2}$
Step 2: Find intersection points
$$y + 1 = \frac{y^2 - 6}{2}$$
$$2y + 2 = y^2 - 6$$
$$y^2 - 2y - 8 = 0$$
$$(y - 4)(y + 2) = 0$$
$$y = -2, \quad y = 4$$
Step 3: Determine which is on the right
At $y = 0$: $x = 1$ (line) and $x = -3$ (parabola)
The line $x = y + 1$ is on the right.
Step 4: Set up and evaluate
$$A = \int_{-2}^{4} \left[(y + 1) - \frac{y^2 - 6}{2}\right] dy$$
$$= \int_{-2}^{4} \left(y + 1 - \frac{y^2}{2} + 3\right) dy$$
$$= \int_{-2}^{4} \left(y + 4 - \frac{y^2}{2}\right) dy$$
$$= \left[\frac{y^2}{2} + 4y - \frac{y^3}{6}\right]_{-2}^{4}$$
At $y = 4$: $8 + 16 - \frac{64}{6} = 24 - \frac{32}{3} = \frac{40}{3}$
At $y = -2$: $2 - 8 + \frac{8}{6} = -6 + \frac{4}{3} = -\frac{14}{3}$
$$A = \frac{40}{3} - \left(-\frac{14}{3}\right) = \frac{54}{3} = 18$$
$$\boxed{A = 18}$$
Problem: Find the area of the region bounded by $y = \sqrt{x}$, $y = 0$, and $x = 4$.
The region is bounded:
- Above by $y = \sqrt{x}$
- Below by $y = 0$ (the x-axis)
- On the right by $x = 4$
The curves meet at $(0, 0)$ and the boundary extends to $x = 4$.
$$A = \int_0^4 [\sqrt{x} - 0] \, dx$$
$$= \int_0^4 x^{1/2} \, dx$$
$$= \left[\frac{2}{3}x^{3/2}\right]_0^4$$
$$= \frac{2}{3}(8) - 0 = \frac{16}{3}$$
$$\boxed{A = \frac{16}{3}}$$
Problem: Find the area between $y = \sin x$ and $y = \cos x$ from $x = 0$ to $x = \frac{\pi}{2}$.
Step 1: Find where they intersect
$$\sin x = \cos x$$
$$\tan x = 1$$
$$x = \frac{\pi}{4}$$
Step 2: Determine which is on top
On $[0, \frac{\pi}{4}]$: $\cos x > \sin x$
On $[\frac{\pi}{4}, \frac{\pi}{2}]$: $\sin x > \cos x$
Step 3: Set up two integrals
$$A = \int_0^{\pi/4} (\cos x - \sin x) \, dx + \int_{\pi/4}^{\pi/2} (\sin x - \cos x) \, dx$$
First integral: $$[\sin x + \cos x]_0^{\pi/4} = \left(\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}\right) - (0 + 1) = \sqrt{2} - 1$$
Second integral: $$[-\cos x - \sin x]_{\pi/4}^{\pi/2} = (0 - 1) - \left(-\frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2}\right) = -1 + \sqrt{2}$$
$$A = (\sqrt{2} - 1) + (\sqrt{2} - 1) = 2\sqrt{2} - 2$$
$$\boxed{A = 2(\sqrt{2} - 1) \approx 0.828}$$
Common Mistakes and Misunderstandings
❌ Mistake: Subtracting in the wrong order
Wrong: $A = \int_a^b [g(x) - f(x)] \, dx$ when $f(x)$ is on top.
Why it's wrong: You'll get a negative area, which doesn't make sense geometrically.
Correct: Always subtract (top − bottom) or (right − left). If unsure, take the absolute value: $A = \int |f(x) - g(x)| \, dx$.
❌ Mistake: Using the wrong limits of integration
Wrong: Using arbitrary bounds instead of finding where the curves intersect.
Why it's wrong: The "enclosed region" is defined by where the curves meet!
Correct: Solve $f(x) = g(x)$ to find the intersection points. These are usually your limits.
❌ Mistake: Using one integral when curves switch positions
Wrong: $A = \int_{-1}^{1} (x - x^3) \, dx$ for the area between $y = x$ and $y = x^3$.
Why it's wrong: On $[-1, 0]$, the cubic is above the line, but on $[0, 1]$, the line is above. Using one integral gives the wrong answer (often zero!).
Correct: Split into two integrals where the "top" curve changes.
❌ Mistake: Not considering integration with respect to y
Wrong: Setting up a complicated multi-part integral with respect to $x$ when integrating with respect to $y$ would be simpler.
Why it's wrong: Sometimes horizontal slices are much easier than vertical slices.
Correct: If the curves are easier to express as $x = g(y)$, or if vertical slices require splitting, try integrating with respect to $y$ using (right − left).
Area Between Curves (Vertical Slices)
Area between two curves where f(x) ≥ g(x). Integrate (top minus bottom) from left to right.
Variables:
- $A$:
- area of the region
- $f(x)$:
- the top curve
- $g(x)$:
- the bottom curve
- $a, b$:
- x-coordinates where the curves intersect (or given bounds)
Area Between Curves (Horizontal Slices)
Area between two curves integrating with respect to y. Use (right minus left) from bottom to top.
Variables:
- $A$:
- area of the region
- $f(y)$:
- the right curve (as x = f(y))
- $g(y)$:
- the left curve (as x = g(y))
- $c, d$:
- y-coordinates where the curves intersect (or given bounds)
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.