Polynomial Functions for MATH 140
Exam Relevance for MATH 140
Polynomial functions are foundational in MATH 140. Properties should be known from precalculus.
What is a Polynomial Function?
Think of polynomials as the "building blocks" of functions — like how LEGO bricks can only snap together in certain ways, polynomials are functions built using only the simplest operations: adding, subtracting, and multiplying powers of $x$.
Here's the key: every exponent on $x$ must be a whole number (0, 1, 2, 3, ...). That's the only rule!
The general form looks like this:
$$f(x) = a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0$$
For example, $f(x) = 3x^4 - 2x^2 + 5x - 7$ is a polynomial. Each term has $x$ raised to a whole number power (4, 2, 1, and 0).
Good news: Recognizing polynomials is really not hard at all! By the end of this lesson, you'll be able to instantly spot whether something is a polynomial or not. We'll give you many examples to make this second nature.
Why does this matter? Being able to quickly identify polynomials will drastically change how you can treat a function in calculus. Polynomials are special — they behave predictably, they're easy to differentiate and integrate, and they have no "surprises" like asymptotes or undefined points.
Why Polynomials Are Special in Calculus
Polynomials have remarkable properties that make them the "friendliest" functions in calculus:
- No domain restrictions — they work for every real number
- No asymptotes — they never shoot off to infinity at a single point
- No holes or breaks — they're continuous everywhere
- Predictable end behavior — their long-term behavior is entirely determined by just two numbers (the degree and leading coefficient)
- Easy calculus operations — derivatives and integrals just use the power rule
Because of these properties, we use polynomials throughout calculus. When functions get messy (like $e^x$, $\sin x$, or $\ln x$), we often approximate them using polynomials (this is called Taylor series). That's actually how your calculator computes values like $e^{2.5}$ or $\sin(0.7)$!
Key Vocabulary
| Term | Meaning | Example |
|---|---|---|
| Degree | The highest power of $x$ with a non-zero coefficient | In $4x^3 - x + 2$, the degree is 3 |
| Leading coefficient | The coefficient of the highest-degree term | In $4x^3 - x + 2$, the leading coefficient is 4 |
| Constant term | The term with no $x$ (the $a_0$ term) | In $4x^3 - x + 2$, the constant term is 2 |
| Monomial | A polynomial with one term | $5x^3$ |
| Binomial | A polynomial with two terms | $x^2 + 1$ |
| Trinomial | A polynomial with three terms | $x^2 + 3x - 7$ |
Examples of Polynomial Functions
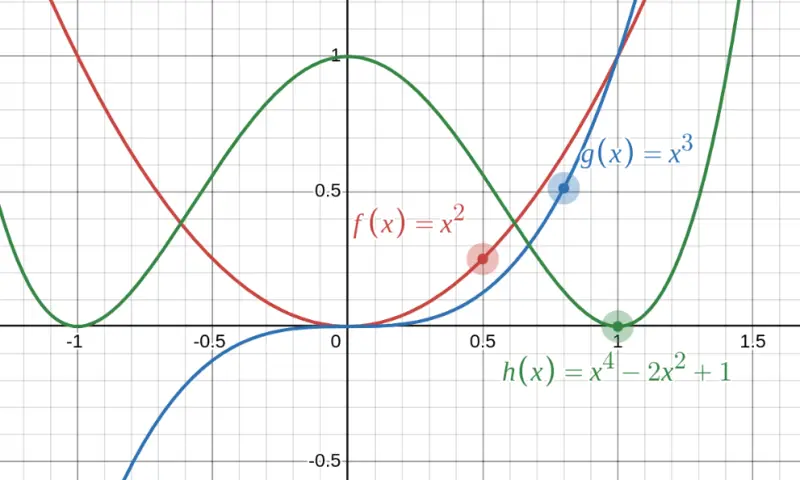
Notice how these graphs are all smooth curves with no breaks, holes, or sharp corners. They're defined everywhere, and they all eventually head toward $+\infty$ or $-\infty$ as you move left or right.
| Function | Degree | Type | Notes |
|---|---|---|---|
| $f(x) = 5$ | 0 | Constant | Horizontal line |
| $f(x) = 2x + 1$ | 1 | Linear | Straight line |
| $f(x) = x^2 - 4x + 3$ | 2 | Quadratic | Parabola |
| $f(x) = x^3$ | 3 | Cubic | S-shaped curve |
| $f(x) = x^4 - x^2$ | 4 | Quartic | W-shaped or U-shaped |
What Makes Something a Polynomial?
A function is a polynomial if every term has $x$ raised to a non-negative integer power (0, 1, 2, 3, ...).
✓ These ARE Polynomials
- $f(x) = x^3 - 2x + 7$ — powers are 3, 1, and 0 (all whole numbers ✓)
- $g(x) = 4$ — this is $4x^0$, a constant polynomial (degree 0 ✓)
- $h(x) = \frac{1}{2}x^4 - \frac{3}{5}x^2 + \pi$ — fractional and irrational coefficients are fine! Only the exponents matter.
What is NOT a Polynomial?
A function is not a polynomial if it has:
- Negative exponents — like $x^{-1} = \frac{1}{x}$
- Fractional exponents — like $x^{1/2} = \sqrt{x}$
- Non-integer exponents — like $x^{2.1}$
- Variables in the denominator — like $\frac{1}{x+1}$
- Variables in the exponent — like $2^x$ or $e^x$
- Transcendental functions — like $\sin x$, $\cos x$, $\ln x$
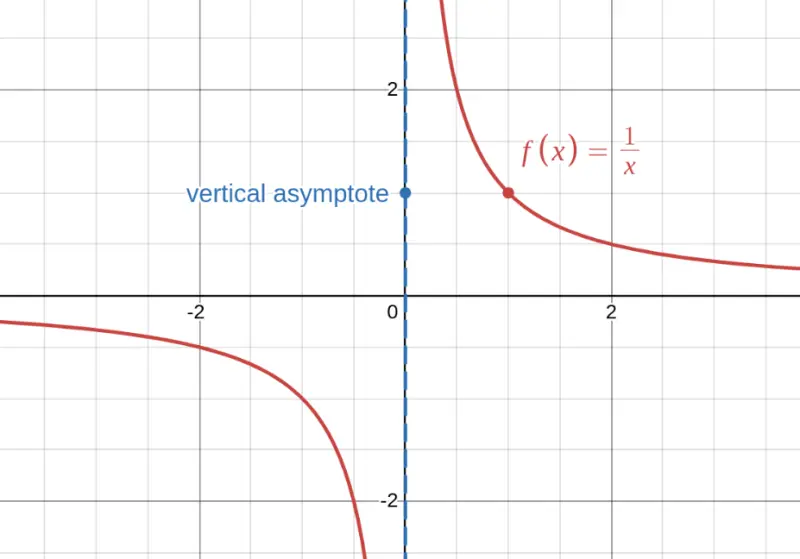
The function $f(x) = \frac{1}{x} = x^{-1}$ is NOT a polynomial because the exponent is $-1$ (negative). Notice the vertical asymptote at $x = 0$ — polynomials never have asymptotes!
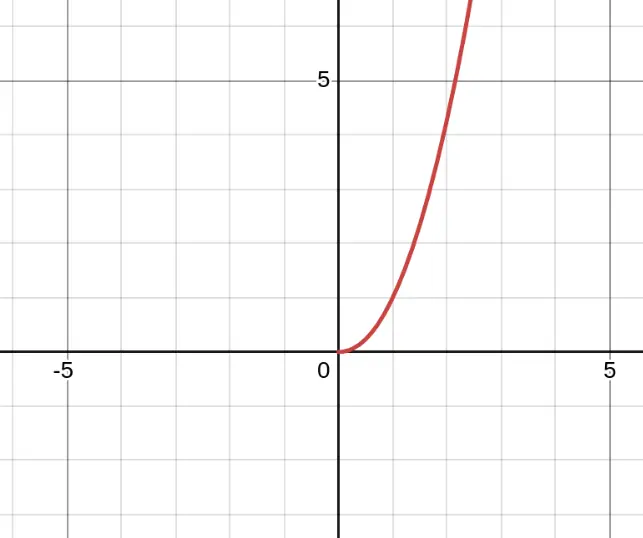
The function $f(x) = x^{2.1}$ is NOT a polynomial because the exponent is $2.1$ (not a whole number). It looks similar to $x^2$, but the non-integer exponent means it's not defined for negative $x$ values and behaves differently in calculus.
Can You Tell From a Graph?
Sometimes you can spot that a function is NOT a polynomial just by looking at its graph. Here are some visual "red flags":
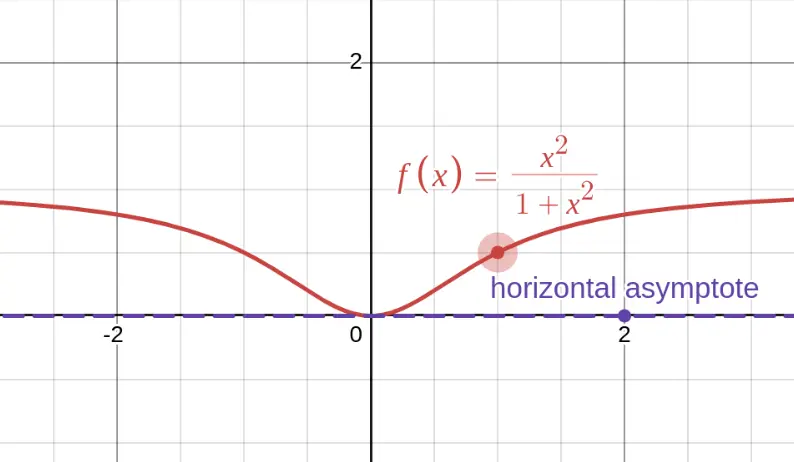
Is this a polynomial? It looks smooth and well-behaved, but notice it levels off as $x \to \pm\infty$ (horizontal asymptote at $y = 1$). Polynomials always go to $\pm\infty$ at the ends — they never flatten out. So this is NOT a polynomial!
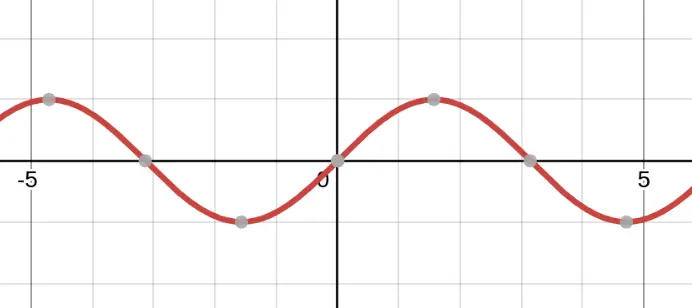
Is this a polynomial? It's smooth everywhere, but it oscillates forever. Polynomials never wiggle back and forth infinitely — they eventually "pick a direction" and head to $\pm\infty$. So this is NOT a polynomial!
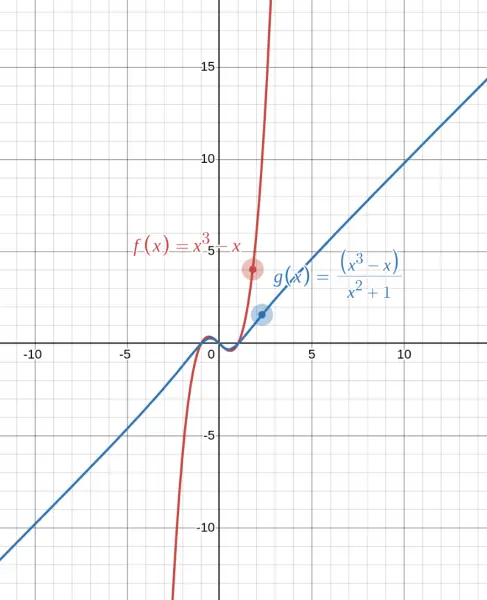
Compare the polynomial $f(x) = x^3 - x$ (blue) with $g(x) = \frac{x^3 - x}{x^2 + 1}$ (red). Both look smooth and similar near $x = 0$, but watch what happens at the ends! The polynomial shoots off to $\pm\infty$, while the other function grows more slowly.
Quick Visual Test: Is It a Polynomial?
| Red Flag | Why It's Not a Polynomial |
|---|---|
| Graph has a vertical asymptote | Polynomials are defined everywhere |
| Graph has a horizontal asymptote | Polynomials always go to $\pm\infty$ at the ends |
| Graph has a hole | Polynomials have no undefined points |
| Graph oscillates infinitely | Polynomials don't wiggle forever |
| Graph has a sharp corner | Polynomials are smooth everywhere |
| Graph only defined for $x \geq 0$ | Polynomials work for all real $x$ |
End Behavior of Polynomials
Every polynomial eventually goes to $+\infty$ or $-\infty$ as $x \to \pm\infty$. The degree and leading coefficient completely determine this:
| Degree | Leading Coeff | As $x \to +\infty$ | As $x \to -\infty$ | Example |
|---|---|---|---|---|
| Even | Positive | $+\infty$ | $+\infty$ | $f(x) = x^2$ |
| Even | Negative | $-\infty$ | $-\infty$ | $f(x) = -x^4$ |
| Odd | Positive | $+\infty$ | $-\infty$ | $f(x) = x^3$ |
| Odd | Negative | $-\infty$ | $+\infty$ | $f(x) = -x^5$ |
Even degree, positive leading coefficient: $f(x) = x^2$ — both ends go UP (like a smile 😊)
Even degree, negative leading coefficient: $f(x) = -x^4$ — both ends go DOWN (like a frown 😞)
Odd degree, positive leading coefficient: $f(x) = x^3$ — falls left, rises right (like a slide going up ↗)
Odd degree, negative leading coefficient: $f(x) = -x^5$ — rises left, falls right (like a slide going down ↘)
This predictability is one reason polynomials are so useful in calculus!
Practice: Classify Each Function
Problem: Is $f(x) = 3x^4 - 2x^2 + x - 5$ a polynomial?
Check each term:
- $3x^4$: exponent is 4 ✓
- $-2x^2$: exponent is 2 ✓
- $x$: exponent is 1 ✓
- $-5$: exponent is 0 ✓
All exponents are non-negative integers.
$$\boxed{\text{Yes, this is a polynomial (degree 4)}}$$
Problem: Is $g(x) = x^2 + \frac{1}{x}$ a polynomial?
Rewrite: $g(x) = x^2 + x^{-1}$
The term $x^{-1}$ has a negative exponent.
$$\boxed{\text{No, this is NOT a polynomial}}$$
Problem: Is $h(x) = 5x^3 - x^{2.5} + 2$ a polynomial?
The term $x^{2.5}$ has a non-integer exponent.
$$\boxed{\text{No, this is NOT a polynomial}}$$
Problem: Is $p(x) = \frac{x^3 + 2x}{x}$ a polynomial?
Simplify first: $p(x) = \frac{x^3 + 2x}{x} = \frac{x(x^2 + 2)}{x} = x^2 + 2$ (for $x \neq 0$)
Careful! The simplified form looks like a polynomial, but there's a hole at $x = 0$ because the original function is undefined there.
$$\boxed{\text{No, this is NOT a polynomial (has a hole at } x=0\text{)}}$$
Problem: Is $q(x) = \pi x^5 - ex^2 + \sqrt{2}$ a polynomial?
Check each term:
- $\pi x^5$: coefficient is $\pi$, exponent is 5 ✓
- $-ex^2$: coefficient is $-e$, exponent is 2 ✓
- $\sqrt{2}$: this is $\sqrt{2} \cdot x^0$, exponent is 0 ✓
Irrational coefficients like $\pi$, $e$, and $\sqrt{2}$ are perfectly fine! Only the exponents need to be whole numbers.
$$\boxed{\text{Yes, this is a polynomial (degree 5)}}$$
Problem: Is it possible that this graph represents a polynomial?

No! Look at the ends of the graph — it flattens out toward $y = 0$ on the left and $y = 1$ on the right. These are horizontal asymptotes.
Polynomials never have horizontal asymptotes. They always go to $+\infty$ or $-\infty$ at the ends, never leveling off at a finite value.
$$\boxed{\text{No, this cannot be a polynomial}}$$
Common Mistakes and Misunderstandings
❌ Mistake: Confusing coefficients with exponents
Wrong: "$f(x) = \frac{1}{2}x^3$ is not a polynomial because of the fraction"
Why it's wrong: The $\frac{1}{2}$ is a coefficient (multiplying the term), not an exponent. Coefficients can be any real number — fractions, irrational numbers, whatever!
Correct: Only the exponents must be non-negative integers. The coefficient $\frac{1}{2}$ is fine, so $\frac{1}{2}x^3$ is a valid polynomial term.
❌ Mistake: Thinking simplifying changes the function
Wrong: "$\frac{x^2 - 1}{x - 1} = x + 1$, so it's a polynomial"
Why it's wrong: The original function has a hole at $x = 1$ (where the denominator is zero). Algebraic simplification doesn't remove that hole — the function is still undefined at $x = 1$.
Correct: The original function $\frac{x^2 - 1}{x - 1}$ is NOT a polynomial because it has a point where it's undefined. Polynomials are defined for ALL real numbers.
❌ Mistake: Assuming all smooth functions are polynomials
Wrong: "$e^x$ is smooth and continuous, so it must be a polynomial"
Why it's wrong: Many functions are smooth but not polynomials. The function $e^x$ has the variable in the exponent, not the base.
Correct: Check whether each term has $x$ raised to a non-negative integer power. For $e^x$, the variable is in the exponent position, so it's NOT a polynomial.
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.