Growth and decay for MATH 140
Exam Relevance for MATH 140
Growth and decay problems appear in MATH 140 applications. Set up and solve y' = ky type differential equations.
The Most Important Equation You've Never Heard Of
In 1965, Intel co-founder Gordon Moore made a prediction: the number of transistors on a computer chip would double approximately every two years.
| Year | Transistors on a chip |
|---|---|
| 1971 | 2,300 |
| 1980 | 30,000 |
| 1990 | 1,000,000 |
| 2000 | 42,000,000 |
| 2010 | 2,000,000,000 |
| 2020 | 50,000,000,000 |
This prediction — "Moore's Law" — has held remarkably true for over 50 years. It's why the smartphone in your pocket has more computing power than all of NASA had when they landed on the moon.
But here's what's fascinating: Moore didn't need to know anything about semiconductor physics to make this prediction. He just needed one equation:
$$A(t) = A_0 \cdot b^{t}$$
This is the exponential growth model, and it describes everything from computer chips to bacteria colonies to your retirement savings. Master this equation, and you can predict the future.
The Exponential Growth Model
When a quantity grows by a constant percentage over equal time intervals, it follows exponential growth:
$$A(t) = A_0 \cdot b^{t}$$
Where:
- $A(t)$ = the amount at time $t$
- $A_0$ = the initial amount (at $t = 0$)
- $b$ = the growth factor (how much it multiplies per time unit)
- $t$ = time
The key insight: Each time period, the quantity multiplies by the same factor, rather than adding the same amount.
Growth Factor vs. Growth Rate
These two are related but different:
Growth rate ($r$): The percentage increase per time period
Growth factor ($b$): What you multiply by: $b = 1 + r$
| Growth rate ($r$) | Growth factor ($b$) | Meaning |
|---|---|---|
| 5% = 0.05 | 1.05 | Grows by 5% each period |
| 100% = 1.00 | 2.00 | Doubles each period |
| 7% = 0.07 | 1.07 | Grows by 7% each period |
So the model can also be written as:
$$A(t) = A_0 \cdot (1 + r)^{t}$$
Example: A population of 1,000 bacteria grows by 15% per hour.
- $A_0 = 1000$
- $r = 0.15$, so $b = 1.15$
- $A(t) = 1000 \cdot (1.15)^t$
After 10 hours: $A(10) = 1000 \cdot (1.15)^{10} \approx 4,046$ bacteria
The Exponential Decay Model
When a quantity decreases by a constant percentage, we get exponential decay:
$$A(t) = A_0 \cdot b^{t} \quad \text{where } 0 < b < 1$$
Or equivalently:
$$A(t) = A_0 \cdot (1 - r)^{t}$$
Where $r$ is the decay rate (the percentage lost per time period).
| Decay rate ($r$) | Decay factor ($b$) | Meaning |
|---|---|---|
| 10% = 0.10 | 0.90 | Loses 10% each period |
| 50% = 0.50 | 0.50 | Halves each period |
| 3% = 0.03 | 0.97 | Loses 3% each period |
Example: A car worth 30,000 dollars depreciates by 12% per year.
- $A_0 = 30000$
- $r = 0.12$, so $b = 0.88$
- $A(t) = 30000 \cdot (0.88)^t$
After 5 years: $A(5) = 30000 \cdot (0.88)^5 \approx 15{,}837$ dollars
The Natural Exponential Model
In many real-world applications, especially in science, we use base $e$:
$$A(t) = A_0 \cdot e^{kt}$$
Where:
- $k > 0$ means growth
- $k < 0$ means decay
- $|k|$ is called the continuous growth/decay rate
Why base $e$?
- It arises naturally from continuous compounding
- The calculus is cleaner: $\frac{d}{dt}[e^{kt}] = k \cdot e^{kt}$
- Many natural processes (radioactive decay, population growth, cooling) naturally follow this form
The two forms are equivalent — you can always convert between them: $$A_0 \cdot b^t = A_0 \cdot e^{kt} \quad \text{where } k = \ln(b)$$
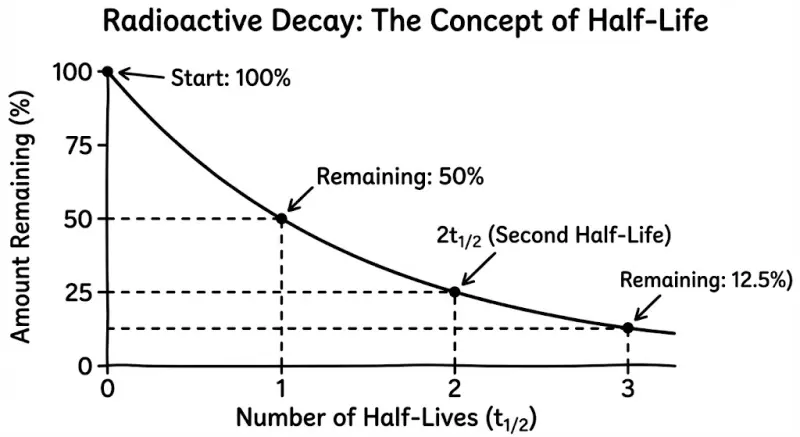
Half-Life: The Signature of Decay
Half-life is the time it takes for a quantity to reduce to half its value.
This is the go-to concept for radioactive decay, but it applies to anything that decays exponentially.
Finding Half-Life from the Decay Constant
If $A(t) = A_0 \cdot e^{kt}$ (where $k < 0$), the half-life is:
$$t_{1/2} = \frac{\ln(2)}{|k|} = \frac{0.693}{|k|}$$
Using Half-Life in Problems
If you know the half-life, you can write the decay model as:
$$A(t) = A_0 \cdot \left(\frac{1}{2}\right)^{t/t_{1/2}}$$
Example: Carbon-14 has a half-life of 5,730 years.
If a fossil originally had 100 units of C-14:
- After 5,730 years: 50 units remain
- After 11,460 years: 25 units remain
- After 17,190 years: 12.5 units remain
Using the formula: $A(t) = 100 \cdot \left(\frac{1}{2}\right)^{t/5730}$
Doubling Time: The Signature of Growth
Doubling time is the time it takes for a quantity to double.
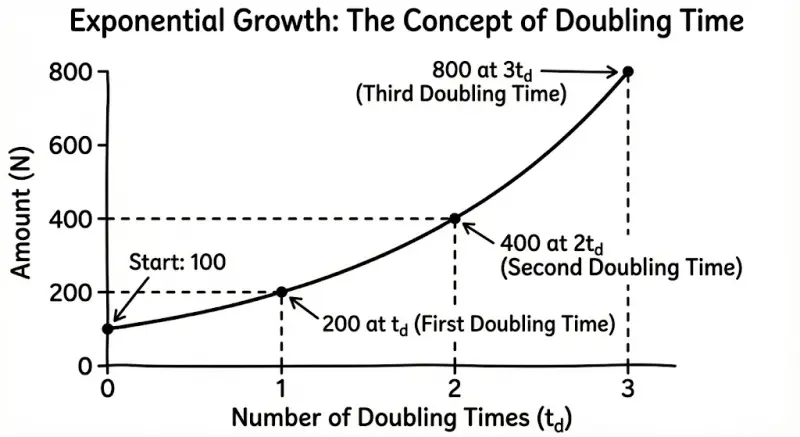
Finding Doubling Time from the Growth Constant
If $A(t) = A_0 \cdot e^{kt}$ (where $k > 0$), the doubling time is:
$$t_{\text{double}} = \frac{\ln(2)}{k} = \frac{0.693}{k}$$
The Rule of 70
A quick approximation: if something grows at $r$% per period, it doubles in approximately:
$$t_{\text{double}} \approx \frac{70}{r}$$
Examples:
- 7% annual growth → doubles in ~10 years
- 10% annual growth → doubles in ~7 years
- 2% annual growth → doubles in ~35 years
This is incredibly useful for quick mental math about investments, populations, or any growing quantity.
Application: Compound Interest
When money earns interest, the interest itself earns interest. This is compound interest — exponential growth applied to money.
Compounding $n$ Times Per Year
$$A(t) = P\left(1 + \frac{r}{n}\right)^{nt}$$
Where:
- $P$ = principal (initial investment)
- $r$ = annual interest rate (as a decimal)
- $n$ = number of times interest compounds per year
- $t$ = time in years
| Compounding | $n$ |
|---|---|
| Annually | 1 |
| Semi-annually | 2 |
| Quarterly | 4 |
| Monthly | 12 |
| Daily | 365 |
Example: 5,000 dollars invested at 6% annual interest, compounded monthly, for 10 years:
$$A = 5000\left(1 + \frac{0.06}{12}\right)^{12 \cdot 10} = 5000(1.005)^{120} \approx 9{,}097$$
Continuous Compounding
What if we compound infinitely often? As $n \to \infty$:
$$A(t) = Pe^{rt}$$
This is continuous compounding — the theoretical maximum growth rate.
Same example with continuous compounding:
$$A = 5000 \cdot e^{0.06 \cdot 10} = 5000 \cdot e^{0.6} \approx 9{,}111$$
Only about 14 dollars more than monthly compounding — the difference is small!
Application: Population Growth
Populations often grow exponentially when resources are abundant:
$$P(t) = P_0 \cdot e^{kt}$$
Example: A city has 500,000 people and is growing at 2.5% per year continuously.
- $P_0 = 500{,}000$
- $k = 0.025$
- $P(t) = 500{,}000 \cdot e^{0.025t}$
When will the population reach 1 million?
$1{,}000{,}000 = 500{,}000 \cdot e^{0.025t}$
$2 = e^{0.025t}$
$\ln(2) = 0.025t$
$t = \frac{\ln(2)}{0.025} \approx 27.7$ years
Application: Radioactive Decay
Radioactive substances decay at a rate proportional to their current amount:
$$A(t) = A_0 \cdot e^{-kt}$$
The decay constant $k$ is related to half-life by: $k = \frac{\ln(2)}{t_{1/2}}$
Carbon Dating
Living organisms contain Carbon-14, which decays with a half-life of 5,730 years. When an organism dies, it stops absorbing new C-14, so the amount decreases.
Example: A fossil contains 30% of its original C-14. How old is it?
$$0.30 = e^{-kt}$$
where $k = \frac{\ln(2)}{5730} \approx 0.000121$
$$\ln(0.30) = -0.000121 \cdot t$$
$$t = \frac{\ln(0.30)}{-0.000121} \approx 9{,}950 \text{ years}$$
Application: Newton's Law of Cooling
When an object is placed in an environment with a different temperature, it cools (or warms) exponentially toward the ambient temperature:
$$T(t) = T_{\text{ambient}} + (T_0 - T_{\text{ambient}}) \cdot e^{-kt}$$
Where:
- $T(t)$ = temperature at time $t$
- $T_{\text{ambient}}$ = surrounding temperature
- $T_0$ = initial temperature of the object
- $k$ = cooling constant (depends on the object and environment)
Example: Coffee at 180°F is placed in a 70°F room. After 10 minutes, it's 120°F. What will it be after 20 minutes?
First, find $k$: $$120 = 70 + (180 - 70)e^{-10k}$$ $$50 = 110e^{-10k}$$ $$e^{-10k} = \frac{50}{110} = \frac{5}{11}$$ $$k = \frac{-\ln(5/11)}{10} \approx 0.0788$$
Now find $T(20)$:
$$T(20) = 70 + 110e^{-0.0788 \cdot 20} = 70 + 110e^{-1.576} \approx 70 + 22.7 \approx 93°F$$
Application: Medicine and Drug Concentration
When you take medication, your body eliminates it exponentially:
$$C(t) = C_0 \cdot e^{-kt}$$
Example: A painkiller has a half-life of 4 hours in the bloodstream. If you take a 500mg dose:
$k = \frac{\ln(2)}{4} \approx 0.173$
After 8 hours: $C(8) = 500 \cdot e^{-0.173 \cdot 8} = 500 \cdot e^{-1.386} \approx 125$ mg
This is why medications have dosing schedules — they're designed to keep the drug concentration within an effective range!
Solving Growth and Decay Problems
Type 1: Find the Amount
Given: initial amount, rate/factor, time
Find: final amount
Just plug into the formula: $$A(t) = A_0 \cdot b^t \quad \text{or} \quad A(t) = A_0 \cdot e^{kt}$$
Type 2: Find the Time
Given: initial amount, final amount, rate/factor
Find: time
Use logarithms:
Starting with $A = A_0 \cdot b^t$:
- Divide: $\frac{A}{A_0} = b^t$
- Take log: $\log_b\left(\frac{A}{A_0}\right) = t$
- Or use natural log: $t = \frac{\ln(A/A_0)}{\ln(b)}$
Type 3: Find the Rate
Given: initial amount, final amount, time
Find: rate
Use logarithms:
Starting with $A = A_0 \cdot e^{kt}$:
- Divide: $\frac{A}{A_0} = e^{kt}$
- Take ln: $\ln\left(\frac{A}{A_0}\right) = kt$
- Solve: $k = \frac{1}{t}\ln\left(\frac{A}{A_0}\right)$
Practice Problems
Problem: A bacteria culture starts with 200 bacteria and triples every 4 hours. How many bacteria are there after 12 hours?
The population triples (×3) every 4 hours.
In 12 hours, there are $\frac{12}{4} = 3$ tripling periods.
$A(12) = 200 \cdot 3^3 = 200 \cdot 27 = 5{,}400$ bacteria
$$\boxed{5{,}400 \text{ bacteria}}$$
Problem: A radioactive substance has a half-life of 8 days. If you start with 100 grams, how much remains after 24 days?
In 24 days, there are $\frac{24}{8} = 3$ half-lives.
$A(24) = 100 \cdot \left(\frac{1}{2}\right)^3 = 100 \cdot \frac{1}{8} = 12.5$ grams
$$\boxed{12.5 \text{ grams}}$$
Problem: An investment of 10,000 dollars earns 5% annual interest, compounded continuously. How long until it reaches 25,000 dollars?
$25000 = 10000 \cdot e^{0.05t}$
$2.5 = e^{0.05t}$
$\ln(2.5) = 0.05t$
$t = \frac{\ln(2.5)}{0.05} = \frac{0.916}{0.05} \approx 18.3$ years
$$\boxed{\approx 18.3 \text{ years}}$$
Problem: Carbon-14 has a half-life of 5,730 years. A sample contains 40% of its original C-14. How old is the sample?
Using $A = A_0 \cdot \left(\frac{1}{2}\right)^{t/5730}$:
$0.40 = \left(\frac{1}{2}\right)^{t/5730}$
$\ln(0.40) = \frac{t}{5730} \cdot \ln(0.5)$
$$t = 5730 \cdot \frac{\ln(0.40)}{\ln(0.5)} = 5730 \cdot \frac{-0.916}{-0.693} \approx 7{,}575 \text{ years}$$
$$\boxed{\approx 7{,}575 \text{ years}}$$
Problem: A population grew from 2,000 to 5,000 over 6 years. Find the continuous growth rate.
$$5000 = 2000 \cdot e^{6k}$$
$$2.5 = e^{6k}$$
$$\ln(2.5) = 6k$$
$$k = \frac{\ln(2.5)}{6} \approx 0.153$$
This is about 15.3% per year.
$$\boxed{k \approx 0.153 \text{ (15.3\% continuous growth rate)}}$$
Problem: How much money should you invest now at 4% annual interest, compounded quarterly, to have 50,000 dollars in 15 years?
We need to find $P$ (present value):
$$50000 = P\left(1 + \frac{0.04}{4}\right)^{4 \cdot 15}$$
$50000 = P(1.01)^{60}$
$50000 = P \cdot 1.8167$
$P = \frac{50000}{1.8167} \approx 27{,}524$ dollars
$$\boxed{27{,}524 \text{ dollars}}$$
Problem: A drug has a half-life of 6 hours. If 400mg is administered, when will only 50mg remain?
$50 = 400 \cdot \left(\frac{1}{2}\right)^{t/6}$
$\frac{50}{400} = \left(\frac{1}{2}\right)^{t/6}$
$0.125 = \left(\frac{1}{2}\right)^{t/6}$
$\left(\frac{1}{2}\right)^3 = \left(\frac{1}{2}\right)^{t/6}$
$3 = \frac{t}{6}$
$t = 18$ hours
$$\boxed{18 \text{ hours}}$$
Problem: Investment A offers 6% annual interest compounded monthly. Investment B offers 5.9% compounded continuously. Which is better for a 10-year investment?
Investment A:
$$A = P(1 + 0.06/12)^{120} = P(1.005)^{120} = 1.8194P$$
Investment B:
$$A = Pe^{0.059 \cdot 10} = Pe^{0.59} = 1.8040P$$
Investment A grows to 1.8194 times the principal. Investment B grows to 1.8040 times the principal.
$$\boxed{\text{Investment A is better (6\% monthly beats 5.9\% continuous)}}$$
Common Mistakes and Misunderstandings
❌ Mistake: Confusing growth rate with growth factor
Wrong: "It grows 5% per year, so $A = A_0 \cdot (0.05)^t$"
Why it's wrong: The 5% is the rate of increase, not the multiplier. If something grows by 5%, you have 100% + 5% = 105% of what you started with.
Correct: $A = A_0 \cdot (1.05)^t$. The growth factor is $1 + r = 1 + 0.05 = 1.05$.
❌ Mistake: Using the wrong sign for decay
Wrong: "It decays at 3% per year, so $A = A_0 \cdot (1.03)^t$"
Why it's wrong: That's growth, not decay! Decay means you're losing 3% each period.
Correct: $A = A_0 \cdot (0.97)^t$ or $A = A_0 \cdot (1 - 0.03)^t$. For decay, the factor is less than 1.
❌ Mistake: Forgetting that half-life means HALF
Wrong: After 2 half-lives, "none remains"
Why it's wrong: After each half-life, half remains. After 2 half-lives, you have $\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}$ remaining, not zero.
Correct: After $n$ half-lives, the fraction remaining is $\left(\frac{1}{2}\right)^n$. The quantity approaches zero but never reaches it.
❌ Mistake: Not matching time units
Wrong: "Interest is 6% per year, invested for 18 months, so $A = P(1.06)^{18}$"
Why it's wrong: The rate is per year, but you used 18 (months) as the exponent. The units must match!
Correct: Either convert time to years: $A = P(1.06)^{1.5}$, or convert rate to monthly: $A = P(1.005)^{18}$.
❌ Mistake: Confusing $A_0$ with $A(t)$
Wrong: Setting up "I have 50,000 dollars now and want to know what I started with" as $50000 \cdot e^{rt} = ?$
Why it's wrong: You're solving for the initial amount, not the final amount. The 50,000 dollars is $A(t)$, not $A_0$.
Correct: $50000 = A_0 \cdot e^{rt}$, so $A_0 = \frac{50000}{e^{rt}}$
Summary: Growth vs. Decay at a Glance
| Exponential Growth | Exponential Decay | |
|---|---|---|
| Formula | $A(t) = A_0 \cdot b^t$ where $b > 1$ | $A(t) = A_0 \cdot b^t$ where $0 < b < 1$ |
| Alternative | $A(t) = A_0 \cdot e^{kt}$ where $k > 0$ | $A(t) = A_0 \cdot e^{kt}$ where $k < 0$ |
| Behavior | Increases without bound | Approaches zero |
| Rate form | $A(t) = A_0(1 + r)^t$ | $A(t) = A_0(1 - r)^t$ |
| Key time | Doubling time: $t = \frac{\ln 2}{k}$ | Half-life: $t = \frac{\ln 2}{|k|}$ |
| Examples | Population, investment, inflation | Radioactive decay, depreciation, cooling |
The Big Picture
Exponential growth and decay are everywhere:
- Your money grows exponentially with compound interest
- Diseases spread exponentially in early stages
- Technology improves exponentially (Moore's Law)
- Radioactive waste decays exponentially over millennia
- Your morning coffee cools exponentially toward room temperature
- Medicine leaves your bloodstream exponentially
The same mathematics describes all of these phenomena. Once you master the exponential model, you have a powerful tool for understanding — and predicting — how quantities change over time.
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.