Infinite Limits for MATH 139
Exam Relevance for MATH 139
Know how to identify vertical asymptotes and determine if limit approaches positive or negative infinity.
This skill appears on:
What is an Infinite Limit?
An infinite limit happens when a function grows without bound (gets infinitely large or infinitely negative) as $x$ approaches some value.
Notation:
- $\displaystyle\lim_{x \to a} f(x) = \infty$ means $f(x)$ grows toward positive infinity
- $\displaystyle\lim_{x \to a} f(x) = -\infty$ means $f(x)$ grows toward negative infinity
Important: Technically, the limit "does not exist" when it's $\pm\infty$, because infinity isn't a real number. But we write $= \infty$ to describe the behavior.
In this graph, we see the function $f(x) = \frac{1}{x}$. Notice how the function shoots up toward $+\infty$ as $x$ approaches $0$ from the right, and plunges down toward $-\infty$ as $x$ approaches $0$ from the left. The y-axis ($x = 0$) is a vertical asymptote.
Vertical Asymptotes
When $\displaystyle\lim_{x \to a} f(x) = \pm\infty$, the line $x = a$ is called a vertical asymptote.
The graph shoots up or down toward this vertical line but never actually touches it.
When Do Infinite Limits Happen?
Infinite limits occur when:
- The denominator approaches 0
- The numerator approaches a non-zero number
$$\frac{\text{non-zero}}{\text{something approaching } 0} \to \pm\infty$$
How to Determine the Sign ($+\infty$ or $-\infty$)
The key question: What's the sign of the function near $x = a$?
Check:
- Is the numerator positive or negative near $a$?
- Is the denominator approaching $0^+$ (small positive) or $0^-$ (small negative)?
$$\frac{(+)}{(0^+)} = +\infty \qquad \frac{(+)}{(0^-)} = -\infty$$ $$\frac{(-)}{(0^+)} = -\infty \qquad \frac{(-)}{(0^-)} = +\infty$$
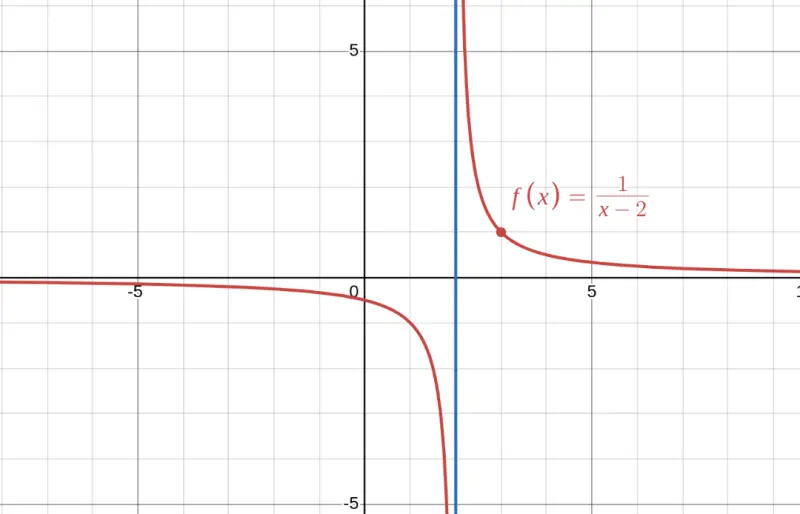
In this graph, we see $f(x) = \frac{1}{x-2}$ with a vertical asymptote at $x = 2$. From the left ($x \to 2^-$), the function goes to $-\infty$. From the right ($x \to 2^+$), it goes to $+\infty$. This is why the two-sided limit DNE.
Problem: Find $\displaystyle\lim_{x \to 2} \frac{1}{(x-2)^2}$
Step 1: What happens to the denominator?
As $x \to 2$: $(x-2)^2 \to 0$
Step 2: What's the sign?
$(x-2)^2$ is always positive (squared term), so the denominator approaches $0^+$.
Step 3: Combine: $$\frac{1}{(0^+)} = +\infty$$
$$\boxed{\lim_{x \to 2} \frac{1}{(x-2)^2} = \infty}$$
Problem: Find $\displaystyle\lim_{x \to 3^+} \frac{2}{x-3}$ and $\displaystyle\lim_{x \to 3^-} \frac{2}{x-3}$
From the right ($x \to 3^+$, so $x > 3$):
- Numerator: $2$ (positive)
- Denominator: $x - 3 > 0$ and $\to 0^+$ $$\frac{2}{0^+} = \boxed{+\infty}$$
From the left ($x \to 3^-$, so $x < 3$):
- Numerator: $2$ (positive)
- Denominator: $x - 3 < 0$ and $\to 0^-$ $$\frac{2}{0^-} = \boxed{-\infty}$$
Since the one-sided limits are different, $\displaystyle\lim_{x \to 3} \frac{2}{x-3}$ DNE.
Problem: Find all vertical asymptotes of $f(x) = \frac{x+1}{x^2-4}$
Step 1: Find where the denominator equals zero: $$x^2 - 4 = 0$$ $$(x-2)(x+2) = 0$$ $$x = 2 \text{ or } x = -2$$
Step 2: Check that the numerator is NOT zero at these points:
- At $x = 2$: numerator $= 2 + 1 = 3 \neq 0$ ✓
- At $x = -2$: numerator $= -2 + 1 = -1 \neq 0$ ✓
Step 3: Vertical asymptotes at $\boxed{x = 2}$ and $\boxed{x = -2}$
Problem: Analyze $f(x) = \frac{x^2-4}{x-2}$
Step 1: Factor: $$\frac{x^2-4}{x-2} = \frac{(x-2)(x+2)}{x-2} = x + 2 \quad (x \neq 2)$$
Step 2: At $x = 2$, both numerator and denominator equal zero.
After canceling, we get $x + 2$, which is defined at $x = 2$.
This means $x = 2$ is a hole (removable discontinuity), NOT a vertical asymptote!
$$\lim_{x \to 2} \frac{x^2-4}{x-2} = 2 + 2 = \boxed{4}$$

In this graph, compare two functions: $f(x) = \frac{1}{x-2}$ (which has a vertical asymptote at $x=2$) and $g(x) = \frac{x^2-4}{x-2}$ (which simplifies to the line $y = x+2$ with a hole at $(2, 4)$). Notice the dramatic difference — one blows up to infinity, the other just has a single missing point!
Key Distinction
| Situation | What Happens | Result |
|---|---|---|
| $\frac{0}{0}$ | Cancel common factor | Usually a hole (finite limit) |
| $\frac{\text{non-zero}}{0}$ | Can't cancel | Vertical asymptote ($\pm\infty$) |
Common Mistakes and Misunderstandings
❌ Mistake: Writing $\lim = \infty$ means the limit "exists"
Wrong thinking: "The limit equals infinity, so it exists."
Why it's wrong: Infinity is not a real number. When we write $\lim_{x \to a} f(x) = \infty$, we're describing behavior, not stating an actual value. The limit technically does not exist (DNE).
Correct: Say "the limit is infinite" or "the limit does not exist (it goes to infinity)."
❌ Mistake: Confusing $\frac{0}{0}$ with $\frac{\text{non-zero}}{0}$
Wrong: "The denominator is zero, so the limit is $\infty$."
Why it's wrong:
- $\frac{0}{0}$ is indeterminate — you need to simplify first (often gives a finite limit or a hole)
- $\frac{\text{non-zero}}{0}$ gives $\pm\infty$ (vertical asymptote)
Correct: Always check BOTH the numerator AND denominator before concluding.
❌ Mistake: Forgetting to check one-sided limits
Wrong: $\displaystyle\lim_{x \to 2} \frac{1}{x-2} = \infty$
Why it's wrong: From the left, it goes to $-\infty$. From the right, it goes to $+\infty$. Since they disagree, the two-sided limit DNE (not just "equals infinity").
Correct: $$\lim_{x \to 2^-} \frac{1}{x-2} = -\infty, \quad \lim_{x \to 2^+} \frac{1}{x-2} = +\infty$$ $$\therefore \lim_{x \to 2} \frac{1}{x-2} \text{ DNE}$$
❌ Mistake: Assuming every zero in the denominator is a vertical asymptote
Wrong: "$f(x) = \frac{x-3}{x-3}$ has a vertical asymptote at $x = 3$."
Why it's wrong: After canceling, $f(x) = 1$ for all $x \neq 3$. There's a hole at $x = 3$, not an asymptote.
Correct: Only $\frac{\text{non-zero}}{0}$ creates a vertical asymptote. If both are zero, factor and simplify first.
❌ Mistake: Getting the sign wrong on one-sided limits
Wrong: $\displaystyle\lim_{x \to 5^-} \frac{3}{x-5} = +\infty$
Why it's wrong: When $x < 5$, we have $x - 5 < 0$, so the denominator is negative. $$\frac{(+)}{(0^-)} = -\infty$$
Correct: $\displaystyle\lim_{x \to 5^-} \frac{3}{x-5} = -\infty$
Tip: Plug in a test value! Try $x = 4.9$: $\frac{3}{4.9-5} = \frac{3}{-0.1} = -30$ (negative!)
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.