Practice Final #1

To differentiate an absolute value function, first determine which "piece" you're on. The expression $|2x - 4|$ changes at $2x - 4 = 0$, which is $x = 2$.

For $x > 2$: the inside $(2x - 4)$ is positive, so $|2x - 4| = 2x - 4$

For $x < 2$: the inside $(2x - 4)$ is negative, so $|2x - 4| = -(2x - 4) = -2x + 4$

Since our anchor point $a = 5$ and our target $x = 4.9$ are both greater than 2, we use:

$$f(x) = 2x - 4$$



$$f(5) = 2(5) - 4 = 10 - 4 = 6$$



Since $f(x) = 2x - 4$ for $x > 2$:

$$f'(x) = 2$$

So $f'(5) = 2$.



Using $L(x) = f(a) + f'(a)(x - a)$:

$$\begin{align*}$$
& L(4.9) = f(5) + f'(5)(4.9 - 5) \\
&= 6 + 2(-0.1) \\
&= 6 - 0.2 \\
&= 5.8
\end{align*}

$$\boxed{f(4.9) \approx 5.8}$$

We use the Product Rule, $(uv)' = u'v + uv'$, where $u = x^{-2}$ and $v = \ln x$.
$$\begin{array}{rl}{\displaystyle }& {\displaystyle f^{\mathrm{\prime }}(x)}\\ {\displaystyle }& {\displaystyle =(-2x^{-3})(\ln x)+(x^{-2})\left(\frac{1}{x}\right)}\\ {\displaystyle }& {\displaystyle =-2x^{-3}\ln x+x^{-3}}\\ {\displaystyle }& {\displaystyle =x^{-3}(1-2\ln x)}\end{array}$$
\begin{aligned}
& \quad f'(x) \\
&= (-2x^{-3})(\ln x) + (x^{-2})\left(\frac{1}{x}\right) \\
&= -2x^{-3} \ln x + x^{-3} \\
&= x^{-3}(1 - 2 \ln x)
\end{aligned}




We set $f'(x) = 0$. Since $x^{-3} = \frac{1}{x^3}$ is never zero for $x > 0$, we solve the other factor:
$$\begin{array}{rl}{\displaystyle 1-2\ln x}& {\displaystyle =0}\\ {\displaystyle 2\ln x}& {\displaystyle =1}\\ {\displaystyle \ln x}& {\displaystyle =\frac{1}{2}}\\ {\displaystyle x}& {\displaystyle =e^{1\mathrm{/}2}}\\ {\displaystyle x}& {\displaystyle =\sqrt{e}}\end{array}$$
\begin{aligned}
1 - 2 \ln x &= 0 \\
2 \ln x &= 1 \\
\ln x &= \frac{1}{2} \\
x &= e^{1/2} \\
x &= \sqrt{e}
\end{aligned}



Since $\sqrt{e} \approx 1.65$, this critical number is within the interval $\left[\frac{1}{2}, 4\right]$.



We use the function $f(x) = \frac{\ln x}{x^2}$ to evaluate the required points.


$$\begin{array}{rl}{\displaystyle }& {\displaystyle f\left(\frac{1}{2}\right)}\\ {\displaystyle }& {\displaystyle =\frac{\ln (1\mathrm{/}2)}{(1\mathrm{/}2{)}^2}}\\ {\displaystyle }& {\displaystyle =\frac{\ln (1)-\ln (2)}{1\mathrm{/}4}}\\ {\displaystyle }& {\displaystyle =4(0-\ln 2)}\\ {\displaystyle }& {\displaystyle =-4\ln 2(\approx -2.77)}\end{array}$$
\begin{aligned}
& \quad f\left(\frac{1}{2}\right) \\
&= \frac{\ln(1/2)}{(1/2)^2} \\
&= \frac{\ln(1) - \ln(2)}{1/4} \\
&= 4(0 - \ln 2) \\
&= -4 \ln 2 \quad (\approx -2.77)
\end{aligned}



$$\begin{array}{rl}{\displaystyle }& {\displaystyle f(4)}\\ {\displaystyle }& {\displaystyle =\frac{\ln 4}{4^2}}\\ {\displaystyle }& {\displaystyle =\frac{\ln 4}{16}(\approx 0.087)}\end{array}$$
\begin{aligned}
& \quad f(4) \\
&= \frac{\ln 4}{4^2} \\
&= \frac{\ln 4}{16} \quad (\approx 0.087)
\end{aligned}



$$\begin{array}{rl}{\displaystyle }& {\displaystyle f(\sqrt{e})}\\ {\displaystyle }& {\displaystyle =\frac{\ln (e^{1\mathrm{/}2})}{(\sqrt{e}{)}^2}}\\ {\displaystyle }& {\displaystyle =\frac{1\mathrm{/}2}{e}}\\ {\displaystyle }& {\displaystyle =\frac{1}{2e}(\approx 0.184)}\end{array}$$
\begin{aligned}
& \quad f(\sqrt{e}) \\
&= \frac{\ln(e^{1/2})}{(\sqrt{e})^2} \\
&= \frac{1/2}{e} \\
&= \frac{1}{2e} \quad (\approx 0.184)
\end{aligned}




Comparing the values $-4 \ln 2$, $\frac{\ln 4}{16}$, and $\frac{1}{2e}$:
- The largest value is $\frac{1}{2e}$.
- The smallest value is $-4 \ln 2$.

We multiply and divide the expression by its conjugate, $(\sqrt{n^2 + 3n} + n)$.
$$\begin{array}{rl}{\displaystyle }& {\displaystyle \underset{n\to \mathrm{\infty }}{\lim }(\sqrt{n^2+3n}-n)}\\ {\displaystyle }& {\displaystyle =\underset{n\to \mathrm{\infty }}{\lim }(\sqrt{n^2+3n}-n)\left(\frac{\sqrt{n^2+3n}+n}{\sqrt{n^2+3n}+n}\right)}\\ {\displaystyle }& {\displaystyle =\underset{n\to \mathrm{\infty }}{\lim }\frac{(n^2+3n)-n^2}{\sqrt{n^2+3n}+n}}\\ {\displaystyle }& {\displaystyle =\underset{n\to \mathrm{\infty }}{\lim }\frac{3n}{\sqrt{n^2+3n}+n}}\end{array}$$
\begin{aligned}
& \quad \lim_{n\to\infty} (\sqrt{n^2 + 3n} - n) \\
&= \lim_{n\to\infty} (\sqrt{n^2 + 3n} - n) \left(\frac{\sqrt{n^2 + 3n} + n}{\sqrt{n^2 + 3n} + n}\right) \\
&= \lim_{n\to\infty} \frac{(n^2 + 3n) - n^2}{\sqrt{n^2 + 3n} + n} \\
&= \lim_{n\to\infty} \frac{3n}{\sqrt{n^2 + 3n} + n}
\end{aligned}


Since $n > 0$, we can simplify $\sqrt{n^2} = n$. We factor $n^2$ out from under the radical in the denominator.
$$\begin{array}{rl}{\displaystyle }& {\displaystyle =\underset{n\to \mathrm{\infty }}{\lim }\frac{3n}{\sqrt{n^2(1+\frac{3}{n})}+n}}\\ {\displaystyle }& {\displaystyle =\underset{n\to \mathrm{\infty }}{\lim }\frac{3\cdot n}{n\sqrt{1+\frac{3}{n}}+n}}\\ {\displaystyle }& {\displaystyle =\underset{n\to \mathrm{\infty }}{\lim }\frac{3\cdot n}{n(\sqrt{1+\frac{3}{n}}+1)}}\\ {\displaystyle }& {\displaystyle =\underset{n\to \mathrm{\infty }}{\lim }\frac{3}{\sqrt{1+\frac{3}{n}}+1}}\end{array}$$
\begin{aligned}
&= \lim_{n\to\infty} \frac{3n}{\sqrt{n^2\left(1 + \frac{3}{n}\right)} + n} \\
&= \lim_{n\to\infty} \frac{3 \cdot n}{n\sqrt{1 + \frac{3}{n}} + n} \\
&= \lim_{n\to\infty} \frac{3 \cdot n}{n\left(\sqrt{1 + \frac{3}{n}} + 1\right)} \\
&= \lim_{n\to\infty} \frac{3}{\sqrt{1 + \frac{3}{n}} + 1}
\end{aligned}

As $n \to \infty$, the term $\frac{3}{n}$ goes to 0.
$$\begin{array}{rl}{\displaystyle }& {\displaystyle =\frac{3}{\sqrt{1+0}+1}}\\ {\displaystyle }& {\displaystyle =\frac{3}{1+1}}\\ {\displaystyle }& {\displaystyle =\boxed{{\displaystyle \frac{3}{2}}}}\end{array}$$
\begin{aligned}
&= \frac{3}{\sqrt{1 + 0} + 1} \\
&= \frac{3}{1 + 1} \\
&= \boxed{\frac{3}{2}}
\end{aligned}

The limit we need to compute is a quotient of two functions, $f(x)$ and $\sqrt{g(x)}$. We try to apply the Quotient Limit Property:

$$\lim_{x \to 0} \frac{f(x)}{\sqrt{g(x)}}$$

The property requires that the limit of the denominator, $\lim_{x \to 0} \sqrt{g(x)}$, exists and is not zero.



We use the Root Limit Property on the denominator:
$$\lim_{x \to c} \sqrt[n]{F(x)} = \sqrt[n]{\lim_{x \to c} F(x)}$$


The key conceptual trick is the Root Limit Property constraint: when $n$ is an even integer (like the square root where $n=2$), the limit of the function inside the root must be non-negative ($\lim_{x \to c} F(x) \geq 0$).


We evaluate the limit of the function inside the square root, $g(x)$:
$$\lim_{x \to 0} g(x) = -4$$

Since the limit value, $-4$, is **negative** and we are taking an **even root** (square root), the Root Limit Property cannot be applied in the real number system.



Since $\lim_{x \to 0} g(x) = -4$, this means that the function $g(x)$ must be negative for values of $x$ sufficiently close to $0$.

Because $g(x) < 0$ near $x=0$, the function $\sqrt{g(x)}$ is **undefined** in the real numbers near $x=0$. Therefore, the overall function $\frac{f(x)}{\sqrt{g(x)}}$ is not defined on any open interval around $x=0$, and the limit **does not exist**.

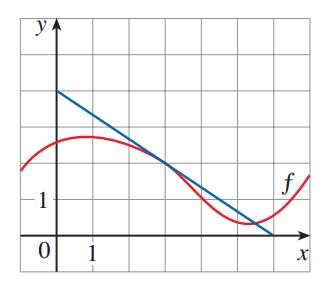
To evaluate $g'(3)$, we first need to find the derivative of $g(x) = \sqrt{f(x)}$. We can rewrite this as $g(x) = (f(x))^{1/2}$. We must use the chain rule to find the derivative.
$$\begin{array}{rl}{\displaystyle }& {\displaystyle g^{\mathrm{\prime }}(x)}\\ {\displaystyle }& {\displaystyle =\frac{1}{2}(f(x){)}^{-1\mathrm{/}2}\cdot f^{\mathrm{\prime }}(x)}\\ {\displaystyle }& {\displaystyle =\frac{f^{\mathrm{\prime }}(x)}{2\sqrt{f(x)}}}\end{array}$$
\begin{aligned}
& \quad g'(x) \\
&= \frac{1}{2}(f(x))^{-1/2} \cdot f'(x) \\
&= \frac{f'(x)}{2\sqrt{f(x)}}
\end{aligned}




Next, we need to find two values from the provided graph: the value of the function $f(3)$ and the slope of the tangent line $f'(3)$ at $x=3$.

From the graph, we can see that the red curve passes through the point $(3, 2)$.
$$\begin{array}{rl}{\displaystyle }& {\displaystyle f(3)}\\ {\displaystyle }& {\displaystyle =2}\end{array}$$
\begin{aligned}
& \quad f(3) \\
&= 2
\end{aligned}

The blue line is the tangent line to the curve at $x=3$. We can find its slope by identifying two points on the line, for example, $(0, 4)$ and $(3, 2)$.
$$\begin{array}{rl}{\displaystyle }& {\displaystyle f^{\mathrm{\prime }}(3)}\\ {\displaystyle }& {\displaystyle =\frac{2-4}{3-0}}\\ {\displaystyle }& {\displaystyle =\frac{-2}{3}}\end{array}$$
\begin{aligned}
& \quad f'(3) \\
&= \frac{2 - 4}{3 - 0} \\
&= \frac{-2}{3}
\end{aligned}




Now we substitute the values we found into the derivative formula from Step 1.
$$\begin{array}{rl}{\displaystyle }& {\displaystyle g^{\mathrm{\prime }}(3)}\\ {\displaystyle }& {\displaystyle =\frac{f^{\mathrm{\prime }}(3)}{2\sqrt{f(3)}}}\\ {\displaystyle }& {\displaystyle =\frac{-2\mathrm{/}3}{2\sqrt{2}}}\\ {\displaystyle }& {\displaystyle =\frac{-2\mathrm{/}3}{2\sqrt{2}}}\\ {\displaystyle }& {\displaystyle =\frac{-1}{3\sqrt{2}}}\\ {\displaystyle }& {\displaystyle =\frac{-1}{3\sqrt{2}}\cdot \frac{\sqrt{2}}{\sqrt{2}}}\\ {\displaystyle }& {\displaystyle =-\frac{\sqrt{2}}{6}}\end{array}$$
\begin{aligned}
& \quad g'(3) \\
&= \frac{f'(3)}{2\sqrt{f(3)}} \\
&= \frac{-2/3}{2\sqrt{2}} \\
&= \frac{-2/3}{2\sqrt{2}} \\
&= \frac{-1}{3\sqrt{2}} \\
&= \frac{-1}{3\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} \\
&= -\frac{\sqrt{2}}{6}
\end{aligned}




$$\begin{array}{rl}{\displaystyle }& {\displaystyle =\boxed{{\displaystyle -\frac{\sqrt{2}}{6}}}}\end{array}$$
\begin{aligned}
&= \boxed{-\frac{\sqrt{2}}{6}}
\end{aligned}

A good anchor point is a "nice" value close to where you're estimating, where you can easily calculate both $f(a)$ and $f'(a)$.

We want to estimate $\ln(0.98)$, so we need an anchor point near $0.98$ where we know the exact value of $\ln$.



Option a) $a = 0$: Can't use this — $\ln(0)$ is undefined!

Option b) $a = 1$: This works! We know $\ln(1) = 0$ exactly, and $1$ is close to $0.98$.

Option c) $a = e$: We know $\ln(e) = 1$, but $e \approx 2.718$ is far from $0.98$. The approximation would be poor.

Option d) $a = 0.98$: This defeats the purpose — we'd need to know $\ln(0.98)$ to use it as an anchor, but that's exactly what we're trying to find!



The best choice is $a = 1$ because:
- $\ln(1) = 0$ is easy to compute
- $1$ is very close to $0.98$

$$\boxed{b) \ a = 1}$$

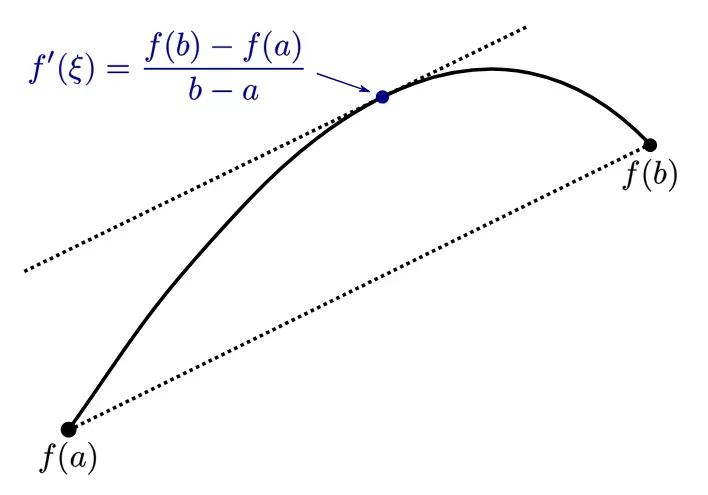
Let $g(x) = 3x^3 - 2x^2 - 6x + 5$. The Mean Value Theorem applied to $g$ on the interval $[-3, 2]$, yields the existence of a number $x_0$ satisfying $-3 < x_0 < 2$ and such that $g'(x_0)$ equals

(a) 17, (b) 20, (c) 27, (d) 35, (e) -2.

This is just a sample. In our question we are using $g(x)$ and instead of $\xi$ we use $x_0$.

The Mean Value Theorem states that if a function $g$ is continuous on a closed interval $[a, b]$ and differentiable on the open interval $(a, b)$, then there exists at least one point $x_0$ in $(a, b)$ such that:

$$g'(x_0) = \frac{g(b) - g(a)}{b - a}$$

The derivative at the special point $x_0$ equals the average rate of change of the function over the entire interval.




$$\begin{align*}$$
& g(x) = 3x^3 - 2x^2 - 6x + 5 \\
& g'(x) = 9x^2 - 4x - 6
\end{align*}




From our previous work, we already know:


$$\begin{align*}$$
& g(-3) = -76 \\
& g(2) = 9
\end{align*}





$$\begin{align*}$$
& \frac{g(2) - g(-3)}{2 - (-3)} = \frac{9 - (-76)}{2 + 3} \\
& \frac{g(2) - g(-3)}{2 - (-3)} = \frac{85}{5} \\
& \frac{g(2) - g(-3)}{2 - (-3)} = 17
\end{align*}


By the Mean Value Theorem, there exists at least one point $x_0$ in the interval $(-3, 2)$ such that $g'(x_0) = 17$.



Looking at the answer choices:
- (a) 17: This matches our calculated value ✓
- (b) 20: Not equal to 17 ✗
- (c) 27: Not equal to 17 ✗
- (d) 35: Not equal to 17 ✗
- (e) -2: Not equal to 17 ✗


$$\boxed{\text{The answer is (a) 17.}}$$

The vertical asymptote(s) of $f(x) = \frac{\sqrt{3x^6 + 7}}{x^3 - 5x^2 + 6x}$ is (are) best described by:

(a) $x = 0$, (b) $x = 2$, (c) $x = 3$, (d) two asymptotes, (e) three asymptotes.



Vertical asymptotes occur at values where the denominator equals zero.

$$\begin{align*}$$
x^3 - 5x^2 + 6x &= 0 \\
x(x^2 - 5x + 6) &= 0 \\
x(x - 2)(x - 3) &= 0
\end{align*}

This gives us $x = 0$, $x = 2$, or $x = 3$ as potential vertical asymptotes.



For these points to be vertical asymptotes, we need to verify that the numerator is non-zero at these points.

The numerator is $\sqrt{3x^6 + 7}$. Since $3x^6$ is always non-negative (as it's raised to an even power) and we're adding the positive constant 7, the expression under the square root is always positive. Therefore, the numerator is always positive and never zero.

Since the numerator is never zero at any of these points, all three values $x = 0$, $x = 2$, and $x = 3$ are vertical asymptotes.



Since we've confirmed that the function has vertical asymptotes at $x = 0$, $x = 2$, and $x = 3$, there are three vertical asymptotes in total.

Therefore:
$$\boxed{\text{The answer is (e) three asymptotes}}$$

When analyzing rational functions with radicals, remember that expressions like $x^{2n} + k$ (where k > 0) are always positive, ensuring that vertical asymptotes occur at all zeros of the denominator.

A function $f(x)$ is continuous at $x = 0$ if:

$$\underset{x\to 0^{-}}{\lim }f(x)=\underset{x\to 0^{+}}{\lim }f(x)=f(0)$$
\lim_{x \to 0^-} f(x) = \lim_{x \to 0^+} f(x) = f(0)




$$f(0)=\cos (0-\pi k)=\cos (\pi k)$$
f(0) = \cos(0 - \pi k) = \cos(\pi k)




$$\underset{x\to 0^{-}}{\lim }f(x)=\cos (\pi k)$$
\lim_{x \to 0^-} f(x) = \cos(\pi k)




Using Taylor expansions:

$$\sin (x)=x-\frac{x^3}{6}+\dots ,\cos (x)=1-\frac{x^2}{2}+\dots$$
\sin(x) = x - \frac{x^3}{6} + \dots, \quad \cos(x) = 1 - \frac{x^2}{2} + \dots


$$\frac{\sin (x)-x}{1-\cos (x)}=\frac{-\frac{x^3}{6}}{\frac{x^2}{2}}=\frac{-x}{3}$$
\frac{\sin(x) - x}{1 - \cos(x)} = \frac{-\frac{x^3}{6}}{\frac{x^2}{2}} = \frac{-x}{3}


Thus:

$$\underset{x\to 0^{+}}{\lim }f(x)=0$$
\lim_{x \to 0^+} f(x) = 0




$$\cos (\pi k)=0$$
\cos(\pi k) = 0




$$\pi k=\frac{\pi }{2},\frac{3\pi }{2},\dots \Rightarrow k=\frac{1}{2},\frac{3}{2},\dots$$
\pi k = \frac{\pi}{2}, \frac{3\pi}{2}, \dots \quad \Rightarrow \quad k = \frac{1}{2}, \frac{3}{2}, \dots


The smallest positive value is:

$$k=\frac{1}{2}$$
k = \frac{1}{2}




$$\boxed{{\displaystyle (B)\hspace{0.17em}k=\frac{1}{2}}}$$
\boxed{(B) \, k = \frac{1}{2}}

$$\ln (1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\dots$$
\ln(1 + x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \dots


Since higher-order terms become negligibly small for small $x$, we approximate:

$$\ln (1+x)\approx x-\frac{x^2}{2}$$
\ln(1 + x) \approx x - \frac{x^2}{2}




$$\frac{1}{\ln (1+x)}=\frac{1}{x-\frac{x^2}{2}}$$
\frac{1}{\ln(1 + x)} = \frac{1}{x - \frac{x^2}{2}}


Factor out $x$:

$$\frac{1}{\ln (1+x)}=\frac{1}{x(1-\frac{x}{2})}$$
\frac{1}{\ln(1 + x)} = \frac{1}{x \left( 1 - \frac{x}{2} \right)}


**Remember:** The approximation $\frac{1}{1 - u} \approx 1 + u$ is useful for small $u$.

Using this approximation:

$$\frac{1}{\ln (1+x)}\approx \frac{1}{x}+\frac{1}{2}$$
\frac{1}{\ln(1 + x)} \approx \frac{1}{x} + \frac{1}{2}




$$\underset{x\to 0}{\lim }((1+\frac{1}{x})-(\frac{1}{x}+\frac{1}{2}))$$
\lim_{x \to 0} \left( \left( 1 + \frac{1}{x} \right) - \left( \frac{1}{x} + \frac{1}{2} \right) \right)


Simplify:

$$\underset{x\to 0}{\lim }(1+\frac{1}{x}-\frac{1}{x}-\frac{1}{2})=\underset{x\to 0}{\lim }(1-\frac{1}{2})$$
\lim_{x \to 0} \left( 1 + \frac{1}{x} - \frac{1}{x} - \frac{1}{2} \right) = \lim_{x \to 0} \left( 1 - \frac{1}{2} \right)


$$\underset{x\to 0}{\lim }\frac{1}{2}=\frac{1}{2}$$
\lim_{x \to 0} \frac{1}{2} = \frac{1}{2}




The value of the limit is:

$$\boxed{{\displaystyle \frac{1}{2}}}$$
\boxed{\frac{1}{2}}


Thus, the correct answer is:

$$\boxed{{\displaystyle (D)\hspace{0.17em}\frac{1}{2}}}$$
\boxed{(D) \, \frac{1}{2}}




This question is trying to teach you something about the comparative size of these two functions as we get closer to 0.

It turns out that $\frac{x + 1}{x}$ is about $1/2$ bigger than $\frac{1}{\ln(1 + x)}$ as we get close to 0, even though they both approach $\infty$. That's what this question is trying to teach you!

Let $x$ = your distance from the wall.

Looking up at the painting, there are two angles:

$\alpha$ = angle from your eye to the top of the painting

$\beta$ = angle from your eye to the bottom of the painting

The viewing angle is $\theta = \alpha - \beta$.



Since tangent = opposite/adjacent, and we know the heights and want the angles, we use arctangent!

The top is 6 ft above eye level, so:
$$\tan(\alpha) = \frac{6}{x} \quad \Rightarrow \quad \alpha = \arctan\left(\frac{6}{x}\right)$$

The bottom is 2 ft above eye level, so:
$$\tan(\beta) = \frac{2}{x} \quad \Rightarrow \quad \beta = \arctan\left(\frac{2}{x}\right)$$

Therefore:
$$\theta(x) = \arctan\left(\frac{6}{x}\right) - \arctan\left(\frac{2}{x}\right)$$



Using $\frac{d}{dx}\arctan(u) = \frac{u'}{1+u^2}$:

$$\begin{align*} & \theta'(x) = \frac{-6/x^2}{1 + 36/x^2} - \frac{-2/x^2}{1 + 4/x^2} \\ &= \frac{-6}{x^2 + 36} + \frac{2}{x^2 + 4} \end{align*}$$



$$\frac{2}{x^2 + 4} = \frac{6}{x^2 + 36}$$

Cross multiply:
$$2(x^2 + 36) = 6(x^2 + 4)$$

$$2x^2 + 72 = 6x^2 + 24$$

$$48 = 4x^2$$

$$x^2 = 12$$

$$x = \sqrt{12} = 2\sqrt{3}$$



As $x \to 0^+$, you are too close and the viewing angle approaches 0.

As $x \to \infty$, you are too far and the viewing angle approaches 0.

Since $\theta(x) > 0$ for finite positive $x$, the critical point must be a maximum.

$$\boxed{x = 2\sqrt{3} \approx 3.46 \text{ feet}}$$

Let $x$ = your distance from the wall.

Looking up at the painting, there are two angles:

$\alpha$ = angle from your eye to the top of the painting

$\beta$ = angle from your eye to the bottom of the painting

The viewing angle is $\theta = \alpha - \beta$.



Since tangent = opposite/adjacent, and we know the heights and want the angles, we use arctangent!

The top is 6 ft above eye level, so:
$$\tan(\alpha) = \frac{6}{x} \quad \Rightarrow \quad \alpha = \arctan\left(\frac{6}{x}\right)$$

The bottom is 2 ft above eye level, so:
$$\tan(\beta) = \frac{2}{x} \quad \Rightarrow \quad \beta = \arctan\left(\frac{2}{x}\right)$$

Therefore:
$$\theta(x) = \arctan\left(\frac{6}{x}\right) - \arctan\left(\frac{2}{x}\right)$$



Using $\frac{d}{dx}\arctan(u) = \frac{u'}{1+u^2}$:

$$\begin{align*} & \theta'(x) = \frac{-6/x^2}{1 + 36/x^2} - \frac{-2/x^2}{1 + 4/x^2} \\ &= \frac{-6}{x^2 + 36} + \frac{2}{x^2 + 4} \end{align*}$$



$$\frac{2}{x^2 + 4} = \frac{6}{x^2 + 36}$$

Cross multiply:
$$2(x^2 + 36) = 6(x^2 + 4)$$

$$2x^2 + 72 = 6x^2 + 24$$

$$48 = 4x^2$$

$$x^2 = 12$$

$$x = \sqrt{12} = 2\sqrt{3}$$



As $x \to 0^+$, you are too close and the viewing angle approaches 0.

As $x \to \infty$, you are too far and the viewing angle approaches 0.

Since $\theta(x) > 0$ for finite positive $x$, the critical point must be a maximum.

$$\boxed{x = 2\sqrt{3} \approx 3.46 \text{ feet}}$$

We must check the left-hand and right-hand limits for $x \to 2$.



$$\begin{array}{rl}{\displaystyle }& {\displaystyle \underset{x\to 2^{-}}{\lim }f(x)}\\ {\displaystyle }& {\displaystyle =\underset{x\to 2^{-}}{\lim }\frac{3}{x-2}}\\ {\displaystyle }& {\displaystyle =\frac{3}{0^{-}}}\\ {\displaystyle }& {\displaystyle =-\mathrm{\infty }}\end{array}$$
\begin{aligned}
& \quad \lim_{x\to 2^-} f(x) \\
&= \lim_{x\to 2^-} \frac{3}{x-2} \\
&= \frac{3}{0^-} \\
&= -\infty
\end{aligned}

$$\begin{array}{rl}{\displaystyle }& {\displaystyle \underset{x\to 2^{+}}{\lim }f(x)}\\ {\displaystyle }& {\displaystyle =\underset{x\to 2^{+}}{\lim }\frac{3}{x-2}}\\ {\displaystyle }& {\displaystyle =\frac{3}{0^{+}}}\\ {\displaystyle }& {\displaystyle =\mathrm{\infty }}\end{array}$$
\begin{aligned}
& \quad \lim_{x\to 2^+} f(x) \\
&= \lim_{x\to 2^+} \frac{3}{x-2} \\
&= \frac{3}{0^+} \\
&= \infty
\end{aligned}

Since the limits from the left and right are not equal, $\lim_{x\to 2} f(x)$ Does Not Exist (DNE).



$$\begin{array}{rl}{\displaystyle }& {\displaystyle \underset{x\to 2^{-}}{\lim }g(x)}\\ {\displaystyle }& {\displaystyle =\underset{x\to 2^{-}}{\lim }-\frac{3}{x-2}}\\ {\displaystyle }& {\displaystyle =-(\frac{3}{0^{-}})}\\ {\displaystyle }& {\displaystyle =-(-\mathrm{\infty })}\\ {\displaystyle }& {\displaystyle =\mathrm{\infty }}\end{array}$$
\begin{aligned}
& \quad \lim_{x\to 2^-} g(x) \\
&= \lim_{x\to 2^-} -\frac{3}{x-2} \\
&= -(\frac{3}{0^-}) \\
&= -(-\infty) \\
&= \infty
\end{aligned}

$$\begin{array}{rl}{\displaystyle }& {\displaystyle \underset{x\to 2^{+}}{\lim }g(x)}\\ {\displaystyle }& {\displaystyle =\underset{x\to 2^{+}}{\lim }-\frac{3}{x-2}}\\ {\displaystyle }& {\displaystyle =-(\frac{3}{0^{+}})}\\ {\displaystyle }& {\displaystyle =-\mathrm{\infty }}\end{array}$$
\begin{aligned}
& \quad \lim_{x\to 2^+} g(x) \\
&= \lim_{x\to 2^+} -\frac{3}{x-2} \\
&= -(\frac{3}{0^+}) \\
&= -\infty
\end{aligned}

Since the limits from the left and right are not equal, $\lim_{x\to 2} g(x)$ Does Not Exist (DNE).



First, simplify the function $f(x) + g(x)$.
$$\begin{array}{rl}{\displaystyle }& {\displaystyle f(x)+g(x)}\\ {\displaystyle }& {\displaystyle =\frac{3}{x-2}+(-\frac{3}{x-2})}\\ {\displaystyle }& {\displaystyle =0}\end{array}$$
\begin{aligned}
& \quad f(x) + g(x) \\
&= \frac{3}{x-2} + \left(-\frac{3}{x-2}\right) \\
&= 0
\end{aligned}

Now, evaluate the limit of the simplified sum.
$$\begin{array}{rl}{\displaystyle }& {\displaystyle \underset{x\to 2}{\lim }[f(x)+g(x)]}\\ {\displaystyle }& {\displaystyle =\underset{x\to 2}{\lim }[0]}\\ {\displaystyle }& {\displaystyle =\boxed{{\displaystyle 0}}}\end{array}$$
\begin{aligned}
& \quad \lim_{x\to 2} [f(x) + g(x)] \\
&= \lim_{x\to 2} [0] \\
&= \boxed{0}
\end{aligned}




The statement is: Is it always true that $\lim_{x\to a} [f(x) + g(x)] = \lim_{x\to a} f(x) + \lim_{x\to a} g(x)$?

The Limit Law for Sums only applies if the limits of the individual functions, $\lim_{x\to a} f(x)$ and $\lim_{x\to a} g(x)$, both exist.

Based on the results from parts (a) and (b):
- The limit of the sum is $\lim_{x\to 2} [f(x) + g(x)] = 0$.
- The sum of the individual limits is $\lim_{x\to 2} f(x) + \lim_{x\to 2} g(x)$, which is DNE + DNE.

Since DNE + DNE is undefined (or does not exist), it is not equal to 0. Therefore, the statement is **not always true**. It fails when the individual limits do not exist.