Volumes of Solids of Revolution / Method of Cylinders for MATH 122
Exam Relevance for MATH 122
Alternative to disk method. Less commonly tested than rings method.
This skill appears on:
Understanding the Method of Cylindrical Shells
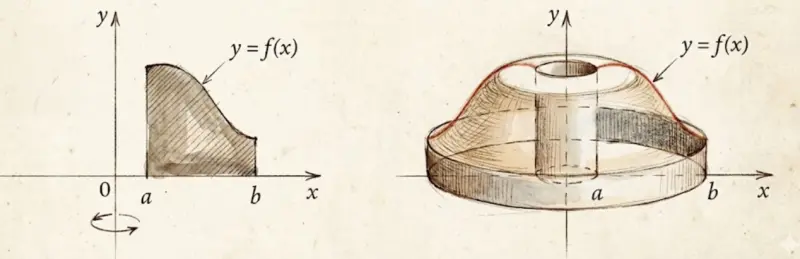
The disk/washer method slices perpendicular to the axis of rotation. But sometimes that's awkward — especially when rotating around the y-axis but the function is easier to express as $y = f(x)$.
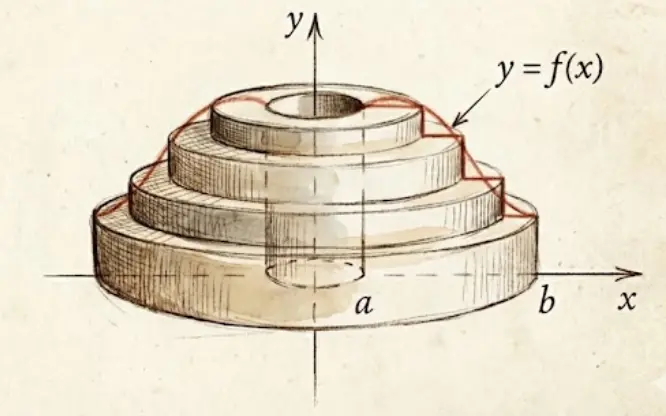
The shell method offers an alternative: instead of slicing into disks, we wrap the region into cylindrical shells (like nested tubes or cans).
The Shell Method Formula
When rotating a region around the y-axis:
$$V = \int_a^b 2\pi x \cdot f(x) \, dx$$
Where does this come from?
Each thin vertical strip at position $x$ with height $f(x)$ and thickness $dx$ becomes a cylindrical shell when rotated:
- Radius = $x$ (distance from the y-axis)
- Height = $f(x)$
- Thickness = $dx$
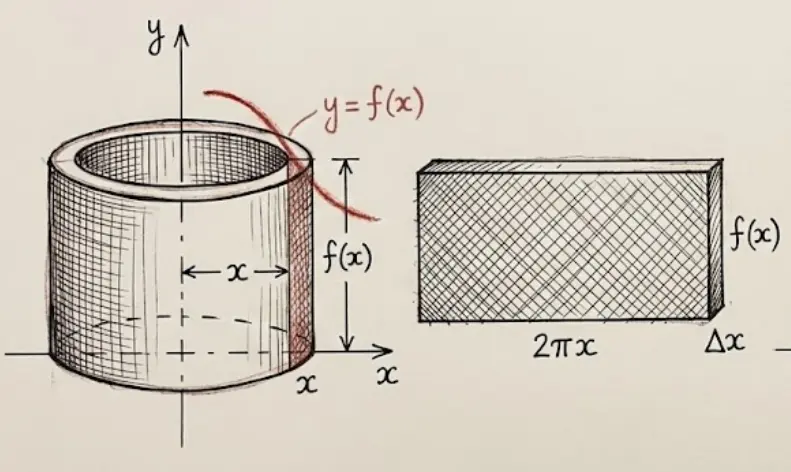
If you "unroll" the shell, you get a thin rectangular slab:
- Length = circumference = $2\pi x$
- Height = $f(x)$
- Thickness = $dx$
Volume of shell = $2\pi x \cdot f(x) \cdot dx$
Getting the volume of a 'shell'

Problem: Find the volume when the region under $y = x^2$ from $x = 0$ to $x = 2$ is rotated around the y-axis.
$$V = \int_0^2 2\pi x \cdot x^2 \, dx = 2\pi \int_0^2 x^3 \, dx$$
$$= 2\pi \left[\frac{x^4}{4}\right]_0^2$$
$$= 2\pi \cdot \frac{16}{4} = 2\pi \cdot 4 = 8\pi$$
$$\boxed{V = 8\pi}$$
Problem: Find the volume when $y = \sqrt{x}$ from $x = 0$ to $x = 4$ is rotated around the y-axis.
$$V = \int_0^4 2\pi x \cdot \sqrt{x} \, dx = 2\pi \int_0^4 x^{3/2} \, dx$$
$$= 2\pi \left[\frac{2}{5}x^{5/2}\right]_0^4$$
$$= 2\pi \cdot \frac{2}{5} \cdot 32 = \frac{128\pi}{5}$$
$$\boxed{V = \frac{128\pi}{5}}$$
With the disk method, you'd need to rewrite as $x = y^2$ and integrate with respect to $y$ — shells are simpler here!
Shells Around the x-axis
When rotating around the x-axis, use horizontal shells:
$$V = \int_c^d 2\pi y \cdot g(y) \, dy$$
where $x = g(y)$ is the width of the shell at height $y$.
Problem: Find the volume when the region bounded by $y = x^2$, $y = 0$, and $x = 1$ is rotated around the x-axis.
Step 1: Express as x = g(y)
From $y = x^2$: $x = \sqrt{y}$
The region goes from $y = 0$ to $y = 1$.
Step 2: Find the shell width
At height $y$, the horizontal strip goes from $x = \sqrt{y}$ to $x = 1$.
Width = $1 - \sqrt{y}$
Step 3: Set up and evaluate
$$V = \int_0^1 2\pi y (1 - \sqrt{y}) \, dy$$
$$= 2\pi \int_0^1 (y - y^{3/2}) \, dy$$
$$= 2\pi \left[\frac{y^2}{2} - \frac{2}{5}y^{5/2}\right]_0^1$$
$$= 2\pi \left(\frac{1}{2} - \frac{2}{5}\right) = 2\pi \cdot \frac{1}{10} = \frac{\pi}{5}$$
$$\boxed{V = \frac{\pi}{5}}$$
Shells with Non-Axis Rotation
When rotating around a vertical line $x = h$:
$$V = \int_a^b 2\pi |x - h| \cdot f(x) \, dx$$
The radius is the distance from the strip to the axis of rotation.
Problem: Find the volume when $y = x^2$ from $x = 0$ to $x = 2$ is rotated around $x = 3$.
Step 1: Find the radius
Distance from $x$ to the line $x = 3$: radius = $3 - x$
Step 2: Set up and evaluate
$$V = \int_0^2 2\pi (3 - x) \cdot x^2 \, dx$$
$$= 2\pi \int_0^2 (3x^2 - x^3) \, dx$$
$$= 2\pi \left[x^3 - \frac{x^4}{4}\right]_0^2$$
$$= 2\pi \left(8 - 4\right) = 2\pi \cdot 4 = 8\pi$$
$$\boxed{V = 8\pi}$$
Problem: Find the volume when the region between $y = x$ and $y = x^2$ is rotated around the y-axis.
Step 1: Find intersection points
$x = x^2$ gives $x = 0$ and $x = 1$.
Step 2: Find the height of each shell
Height = (top) − (bottom) = $x - x^2$
Step 3: Set up and evaluate
$$V = \int_0^1 2\pi x (x - x^2) \, dx$$
$$= 2\pi \int_0^1 (x^2 - x^3) \, dx$$
$$= 2\pi \left[\frac{x^3}{3} - \frac{x^4}{4}\right]_0^1$$
$$= 2\pi \left(\frac{1}{3} - \frac{1}{4}\right) = 2\pi \cdot \frac{1}{12} = \frac{\pi}{6}$$
$$\boxed{V = \frac{\pi}{6}}$$
When to Use Shells vs. Disks/Washers
| Situation | Preferred Method |
|---|---|
| Rotating around y-axis, function is $y = f(x)$ | Shells |
| Rotating around x-axis, function is $x = g(y)$ | Shells |
| Rotating around x-axis, function is $y = f(x)$ | Disks/Washers |
| Rotating around y-axis, function is $x = g(y)$ | Disks/Washers |
| One method requires multiple integrals | Try the other method |
Rule of thumb: If you'd need to solve for the other variable or split into multiple integrals, try switching methods!
Common Mistakes and Misunderstandings
❌ Mistake: Forgetting the $2\pi$ factor
Wrong: $V = \int x \cdot f(x) \, dx$
Why it's wrong: The circumference of each shell is $2\pi r$, not just $r$.
Correct: $V = \int 2\pi x \cdot f(x) \, dx$
❌ Mistake: Using the wrong radius
Wrong: Using $f(x)$ as the radius when rotating around the y-axis.
Why it's wrong: The radius is the distance from the strip to the axis, which is $x$ (not the height of the function).
Correct: For rotation around the y-axis, radius = $x$. For rotation around $x = h$, radius = $|x - h|$.
❌ Mistake: Confusing shell height with shell radius
Wrong: Setting up $V = \int 2\pi f(x) \cdot x \, dx$ with $f(x)$ as radius and $x$ as height.
Why it's wrong: For shells around the y-axis: radius = $x$ (distance to axis), height = $f(x)$ (vertical extent).
Correct: Always identify: What's the distance to the axis? (radius) What's the extent parallel to the axis? (height)
❌ Mistake: Using shells when disks are simpler
Wrong: Forcing the shell method when the disk method would be straightforward.
Why it's wrong: Both methods give the same answer, but one is often much easier. Choose wisely!
Correct: If rotating around the x-axis and $y = f(x)$ is simple, use disks. If rotating around the y-axis and $y = f(x)$ is simple, use shells.
Shell Method (Rotation about y-axis)
Volume when rotating around the y-axis using cylindrical shells. Each shell has radius x, height f(x), and circumference 2πx.
Variables:
- $V$:
- volume of the solid
- $x$:
- radius of the shell (distance to y-axis)
- $f(x)$:
- height of the shell
- $a, b$:
- bounds on the x-axis
Shell Method (Rotation about x-axis)
Volume when rotating around the x-axis using cylindrical shells. Each shell has radius y, width g(y), and circumference 2πy.
Variables:
- $V$:
- volume of the solid
- $y$:
- radius of the shell (distance to x-axis)
- $g(y)$:
- width of the shell (horizontal extent)
- $c, d$:
- bounds on the y-axis
Shell Method (General Axis x = h)
Volume when rotating around a vertical line x = h. The radius is the distance from x to the axis of rotation.
Variables:
- $V$:
- volume of the solid
- $|x - h|$:
- radius (distance from x to axis x = h)
- $f(x)$:
- height of the shell
- $h$:
- the vertical line of rotation
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.