Continuity for MATH 122
Exam Relevance for MATH 122
Foundational concept. Piecewise function continuity may be tested directly.
This skill appears on:
What is Continuity?
Intuitive Definition: A function is continuous if you can draw its graph without lifting your pencil.
If you have to lift your pencil (because of a jump, hole, or asymptote), the function is discontinuous at that point.
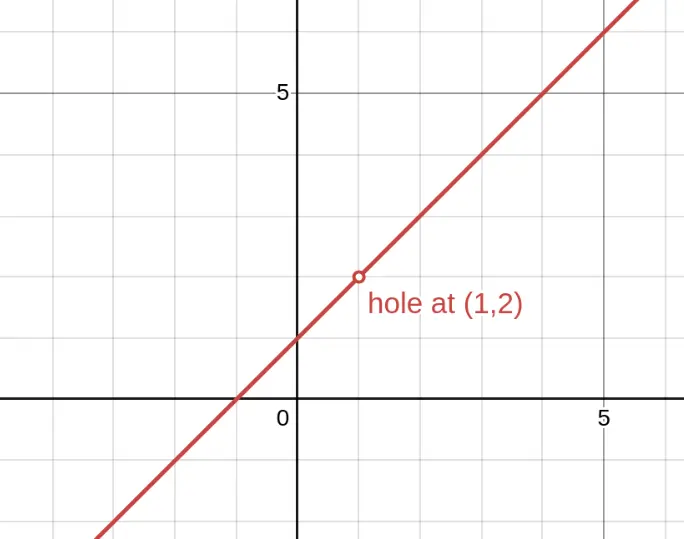
In this graph, we see $f(x) = \frac{x^2-1}{x-1}$, which looks like the line $y = x + 1$ but has a hole at the point $(1, 2)$. The function is discontinuous at $x = 1$ because $f(1)$ is undefined.
The Formal Definition
A function $f$ is continuous at $x = a$ if ALL THREE conditions are met:
| Condition | What to Check |
|---|---|
| 1. $f(a)$ exists | The function is defined at $a$ |
| 2. $\displaystyle\lim_{x \to a} f(x)$ exists | The limit exists (left = right) |
| 3. $\displaystyle\lim_{x \to a} f(x) = f(a)$ | The limit equals the function value |
Memory trick: The limit must exist, the value must exist, and they must be equal!
Types of Discontinuities
1. Removable Discontinuity (Hole)
- The limit exists, but $f(a)$ is either undefined or different from the limit
- Can be "fixed" by redefining $f(a)$
- Graph has a hole (missing point)
2. Jump Discontinuity
- The one-sided limits exist but are different
- $\displaystyle\lim_{x \to a^-} f(x) \neq \lim_{x \to a^+} f(x)$
- Common in piecewise functions
- Graph has a jump between pieces
3. Infinite Discontinuity (Asymptote)
- The limit is $\pm\infty$
- Graph has a vertical asymptote
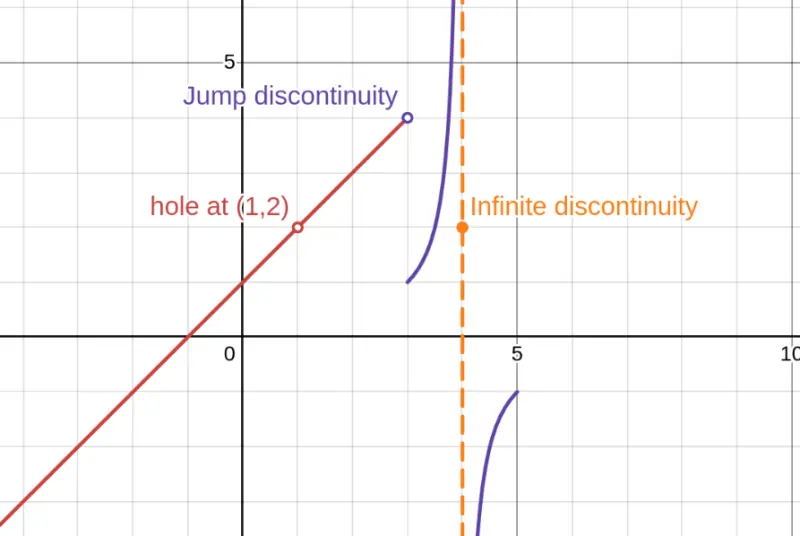
In this graph, we compare the three types: a hole (removable), a jump (piecewise function), and a vertical asymptote (infinite discontinuity).
Functions That Are Always Continuous
These functions are continuous everywhere in their domain:
| Function Type | Example | Where Continuous |
|---|---|---|
| Polynomials | $x^2 + 3x - 5$ | All real numbers |
| Exponentials | $e^x$, $2^x$ | All real numbers |
| Sine/Cosine | $\sin x$, $\cos x$ | All real numbers |
| Rational | $\frac{p(x)}{q(x)}$ | Everywhere except where $q(x) = 0$ |
| Roots | $\sqrt{x}$, $\sqrt[3]{x}$ | Their domain |
| Logarithms | $\ln x$ | $x > 0$ |
Problem: Is $f(x) = \frac{x^2 - 1}{x - 1}$ continuous at $x = 1$?
Step 1: Check if $f(1)$ exists
$$f(1) = \frac{1^2 - 1}{1 - 1} = \frac{0}{0} \quad \text{Undefined!}$$
Condition 1 fails → $f$ is NOT continuous at $x = 1$.
Step 2: Identify the type of discontinuity
Find the limit by factoring: $$\lim_{x \to 1} \frac{x^2-1}{x-1} = \lim_{x \to 1} \frac{(x-1)(x+1)}{x-1} = \lim_{x \to 1} (x+1) = 2$$
The limit exists and equals 2, so this is a removable discontinuity (hole) at the point $(1, 2)$.
Problem: Is $f(x) = \begin{cases} x^2 & \text{if } x < 2 \\ 3x - 2 & \text{if } x \geq 2 \end{cases}$ continuous at $x = 2$?
Step 1: Check all three conditions
Condition 1: Is $f(2)$ defined? $$f(2) = 3(2) - 2 = 4 \quad \checkmark$$
Condition 2: Does the limit exist?
- From the left: $\displaystyle\lim_{x \to 2^-} x^2 = 4$
- From the right: $\displaystyle\lim_{x \to 2^+} (3x-2) = 4$
- Both sides equal 4, so $\displaystyle\lim_{x \to 2} f(x) = 4 \quad \checkmark$
Condition 3: Does limit = function value? $$\lim_{x \to 2} f(x) = 4 = f(2) \quad \checkmark$$
All three conditions pass!
$$\boxed{\text{Yes, } f \text{ is continuous at } x = 2}$$
Problem: Find all discontinuities of $f(x) = \frac{x}{x^2 - 4}$
Step 1: Find where the denominator equals zero
$$x^2 - 4 = 0$$ $$(x-2)(x+2) = 0$$ $$x = 2 \text{ or } x = -2$$
Step 2: Check the numerator at these points
| $x$ value | Numerator | Denominator | Type |
|---|---|---|---|
| $x = 2$ | $2 \neq 0$ | $0$ | Infinite (asymptote) |
| $x = -2$ | $-2 \neq 0$ | $0$ | Infinite (asymptote) |
Since numerator $\neq 0$ at both points, we have $\frac{\text{non-zero}}{0} \to \pm\infty$.
$$\boxed{\text{Vertical asymptotes at } x = 2 \text{ and } x = -2}$$
Problem: Find $k$ so that $f(x) = \begin{cases} x^2 + k & \text{if } x < 1 \\ 2x & \text{if } x \geq 1 \end{cases}$ is continuous at $x = 1$.
Step 1: Set up the continuity requirement
For continuity, the left and right limits must equal each other (and equal $f(1)$): $$\lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x)$$
Step 2: Evaluate each side
- From the left: $\displaystyle\lim_{x \to 1^-} (x^2 + k) = 1^2 + k = 1 + k$
- From the right: $\displaystyle\lim_{x \to 1^+} 2x = 2(1) = 2$
Step 3: Solve for $k$
$$1 + k = 2$$ $$\boxed{k = 1}$$
Common Mistakes and Misunderstandings
❌ Mistake: Checking only ONE condition for continuity
Wrong: "The limit exists, so it's continuous."
Why it's wrong: Continuity requires ALL THREE conditions:
- $f(a)$ exists
- $\lim_{x \to a} f(x)$ exists
- They're equal
A hole has an existing limit but fails condition 1 or 3!
Correct: Always check all three conditions.
❌ Mistake: Confusing "continuous" with "differentiable"
Wrong: "The function is continuous, so I can take its derivative everywhere."
Why it's wrong: Continuity does NOT guarantee differentiability. A function can be continuous but have a sharp corner (like $|x|$ at $x = 0$) where the derivative doesn't exist.
Correct: Differentiable → Continuous (always true), but Continuous → Differentiable (NOT always true).
❌ Mistake: Forgetting to check one-sided limits for piecewise functions
Wrong: Just plugging in $x = a$ into one piece of the function.
Why it's wrong: At the boundary of a piecewise function, you must check BOTH sides approach the same value.
Correct: Always compute $\lim_{x \to a^-}$ and $\lim_{x \to a^+}$ separately, then verify they're equal.
❌ Mistake: Thinking a hole means the limit doesn't exist
Wrong: "$f(x) = \frac{x^2-1}{x-1}$ has a hole at $x=1$, so the limit doesn't exist."
Why it's wrong: A hole means the FUNCTION is undefined, but the LIMIT still exists! The limit is just the y-coordinate of the hole.
Correct: $\displaystyle\lim_{x \to 1} \frac{x^2-1}{x-1} = 2$ (the limit exists, it's the function value that doesn't).
❌ Mistake: Assuming rational functions are always discontinuous
Wrong: "This is a fraction, so it must have discontinuities."
Why it's wrong: Rational functions are continuous everywhere IN THEIR DOMAIN. They're only discontinuous where the denominator equals zero.
Correct: $f(x) = \frac{x^2 + 1}{x^2 + 4}$ is continuous everywhere (denominator is never zero).
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.