chapt 1.11 in clp_2 for UBC math 101 for MATH 101 A

This skill appears on:

winter 2024 Final

Lesson

Why Numerical Integration?

Some integrals can't be evaluated exactly — there's no antiderivative in terms of elementary functions. For example:

$$\int_0^1 e^{-x^2} \, dx$$

Even when we can find the antiderivative, numerical methods are often faster for getting a decimal answer. The three main methods we'll cover are:

Midpoint Rule — rectangles using midpoints
Trapezoidal Rule — trapezoids
Simpson's Rule — parabolic arcs

All three methods work by dividing $[a, b]$ into $n$ equal subintervals of width:

$$\Delta x = \frac{b - a}{n}$$

$Subdivision diagram showing interval $[a,b]$ divided into $n$ subintervals with points $a = x_0, x_1, x_2, \ldots, x_{n-1}, x_n = b$$
Subdivision diagram showing interval $[a,b]$ divided into $n$ subintervals with points $a = x_0, x_1, x_2, \ldots, x_{n-1}, x_n = b$

The Midpoint Rule

Use rectangles whose heights are the function values at the midpoint of each subinterval.

$$M_n = \Delta x \left[f(\bar{x}_1) + f(\bar{x}_2) + \cdots + f(\bar{x}_n)\right]$$

where $\bar{x}_i = \frac{x_{i-1} + x_i}{2}$ is the midpoint of the $i$-th subinterval.

In practice: The midpoints are at $a + \frac{\Delta x}{2}, a + \frac{3\Delta x}{2}, a + \frac{5\Delta x}{2}, \ldots$

Midpoint rectangle showing a single subinterval $[x_{j-1}, x_j]$ with rectangle height $f(\bar{x}_j) = f\left(\frac{x_{j-1}+x_j}{2}\right)$ at the midpoint

Example 1: Midpoint Rule

Problem: Use the Midpoint Rule with $n = 4$ to approximate $\displaystyle\int_0^2 x^2 \, dx$.

$$\Delta x = \frac{2 - 0}{4} = 0.5$$

The subintervals are $[0, 0.5], [0.5, 1], [1, 1.5], [1.5, 2]$.

Midpoints: $\bar{x}_1 = 0.25, \bar{x}_2 = 0.75, \bar{x}_3 = 1.25, \bar{x}_4 = 1.75$

$$M_4 = 0.5\left[f(0.25) + f(0.75) + f(1.25) + f(1.75)\right]$$

$$= 0.5\left[0.0625 + 0.5625 + 1.5625 + 3.0625\right]$$

$$= 0.5 \times 5.25 = 2.625$$

$$\boxed{M_4 = 2.625}$$

The Trapezoidal Rule

Use trapezoids instead of rectangles. Each trapezoid has parallel sides of heights $f(x_{i-1})$ and $f(x_i)$.

$$T_n = \frac{\Delta x}{2}\left[f(x_0) + 2f(x_1) + 2f(x_2) + \cdots + 2f(x_{n-1}) + f(x_n)\right]$$

Notice the pattern: First and last terms have coefficient 1, all middle terms have coefficient 2.

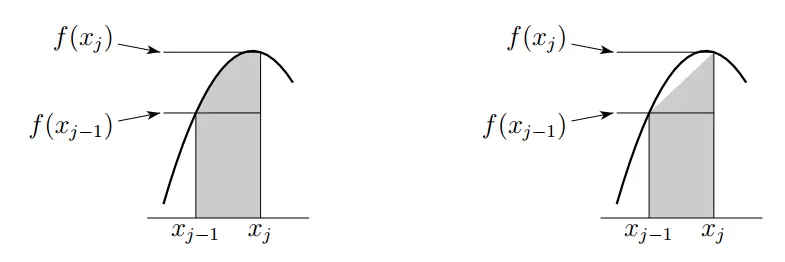
Trapezoid showing a single subinterval $[x_{j-1}, x_j]$ with heights $f(x_{j-1})$ and $f(x_j)$ at the endpoints

Example 2: Trapezoidal Rule

Problem: Use the Trapezoidal Rule with $n = 4$ to approximate $\displaystyle\int_0^2 x^2 \, dx$.

$$\Delta x = \frac{2 - 0}{4} = 0.5$$

The points are: $x_0 = 0, x_1 = 0.5, x_2 = 1, x_3 = 1.5, x_4 = 2$

$$T_4 = \frac{0.5}{2}\left[f(0) + 2f(0.5) + 2f(1) + 2f(1.5) + f(2)\right]$$

$$= 0.25\left[0 + 2(0.25) + 2(1) + 2(2.25) + 4\right]$$

$$= 0.25\left[0 + 0.5 + 2 + 4.5 + 4\right]$$

$$= 0.25 \times 11 = 2.75$$

$$\boxed{T_4 = 2.75}$$

Simpson's Rule

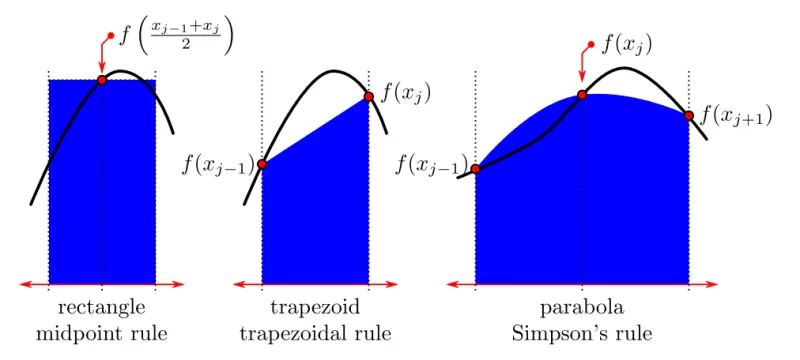
Simpson's Rule uses parabolic arcs instead of straight lines. It's generally the most accurate method.

$$S_n = \frac{\Delta x}{3}\left[f(x_0) + 4f(x_1) + 2f(x_2) + 4f(x_3) + 2f(x_4) + \cdots + 4f(x_{n-1}) + f(x_n)\right]$$

The pattern: Coefficients alternate 1, 4, 2, 4, 2, 4, ..., 4, 1

Important: Simpson's Rule requires $n$ to be even.

Simpson's Rule parabola showing three consecutive points $(x_0, f(x_0))$, $(x_1, f(x_1))$, $(x_2, f(x_2))$ with a parabolic arc passing through them

Example 3: Simpson's Rule

Problem: Use Simpson's Rule with $n = 4$ to approximate $\displaystyle\int_0^2 x^2 \, dx$.

$$\Delta x = \frac{2 - 0}{4} = 0.5$$

The points are: $x_0 = 0, x_1 = 0.5, x_2 = 1, x_3 = 1.5, x_4 = 2$

$$S_4 = \frac{0.5}{3}\left[f(0) + 4f(0.5) + 2f(1) + 4f(1.5) + f(2)\right]$$

$$= \frac{0.5}{3}\left[0 + 4(0.25) + 2(1) + 4(2.25) + 4\right]$$

$$= \frac{0.5}{3}\left[0 + 1 + 2 + 9 + 4\right]$$

$$= \frac{0.5}{3} \times 16 = \frac{8}{3} \approx 2.6667$$

$$\boxed{S_4 = \frac{8}{3} \approx 2.6667}$$

Comparing Results and Computing Error

The exact value is $\displaystyle\int_0^2 x^2 \, dx = \frac{x^3}{3}\Big|_0^2 = \frac{8}{3} \approx 2.6667$.

Method	Approximation	Absolute Error
Midpoint	2.625	0.0417
Trapezoidal	2.75	0.0833
Simpson's	2.6667	0 (exact!)

Surprise: For polynomials of degree ≤ 3, Simpson's Rule gives the exact answer!

Types of Error

When $\alpha$ is an approximation to the true value $A$:

Absolute Error: $$|A - \alpha|$$

Relative Error: $$\frac{|A - \alpha|}{|A|}$$

Percentage Error: $$100 \times \frac{|A - \alpha|}{|A|}\%$$

Example 4: Computing All Error Types

Problem: The Trapezoidal Rule with $n = 4$ gives $T_4 = 2.75$ for $\displaystyle\int_0^2 x^2 \, dx$. The exact value is $\frac{8}{3}$. Find the absolute, relative, and percentage errors.

True value: $A = \frac{8}{3} \approx 2.6667$

Approximation: $\alpha = 2.75$

Absolute Error: $$|A - \alpha| = \left|\frac{8}{3} - 2.75\right| = \left|\frac{8}{3} - \frac{11}{4}\right| = \left|\frac{32 - 33}{12}\right| = \frac{1}{12} \approx 0.0833$$

Relative Error: $$\frac{|A - \alpha|}{|A|} = \frac{1/12}{8/3} = \frac{1}{12} \times \frac{3}{8} = \frac{3}{96} = \frac{1}{32} = 0.03125$$

Percentage Error: $$100 \times 0.03125 = 3.125\%$$

$$\boxed{\text{Absolute: } \frac{1}{12}, \quad \text{Relative: } \frac{1}{32}, \quad \text{Percentage: } 3.125\%}$$

Example 5: Approximating a Non-Elementary Integral

Problem: Use Simpson's Rule with $n = 4$ to approximate $\displaystyle\int_0^1 e^{-x^2} \, dx$.

$$\Delta x = \frac{1 - 0}{4} = 0.25$$

Points: $x_0 = 0, x_1 = 0.25, x_2 = 0.5, x_3 = 0.75, x_4 = 1$

Compute function values:

$f(0) = e^0 = 1$
$f(0.25) = e^{-0.0625} \approx 0.9394$
$f(0.5) = e^{-0.25} \approx 0.7788$
$f(0.75) = e^{-0.5625} \approx 0.5698$
$f(1) = e^{-1} \approx 0.3679$

$$S_4 = \frac{0.25}{3}\left[1 + 4(0.9394) + 2(0.7788) + 4(0.5698) + 0.3679\right]$$

$$= \frac{0.25}{3}\left[1 + 3.7576 + 1.5576 + 2.2792 + 0.3679\right]$$

$$= \frac{0.25}{3} \times 8.9623 \approx 0.7469$$

$$\boxed{S_4 \approx 0.7469}$$

(The actual value is approximately 0.7468, so Simpson's is very accurate even with just $n = 4$!)

Example 6: Using Data from a Table

Problem: Use the Trapezoidal Rule to estimate $\displaystyle\int_0^{1.2} f(x) \, dx$ using:

$x$	0	0.3	0.6	0.9	1.2
$f(x)$	2.0	2.4	2.9	3.1	3.0

$$\Delta x = 0.3, \quad n = 4$$

$$T_4 = \frac{0.3}{2}\left[2.0 + 2(2.4) + 2(2.9) + 2(3.1) + 3.0\right]$$

$$= 0.15\left[2.0 + 4.8 + 5.8 + 6.2 + 3.0\right]$$

$$= 0.15 \times 21.8 = 3.27$$

$$\boxed{T_4 = 3.27}$$

Quick Reference: Coefficient Patterns

Method	Formula Prefix	Coefficient Pattern
Midpoint	$\Delta x$	All 1's (at midpoints)
Trapezoidal	$\frac{\Delta x}{2}$	1, 2, 2, 2, ..., 2, 1
Simpson's	$\frac{\Delta x}{3}$	1, 4, 2, 4, 2, ..., 4, 1

Common Mistakes and Misunderstandings

❌ Mistake: Using endpoints for Midpoint Rule

Wrong: Evaluating $f(x_0), f(x_1), \ldots, f(x_n)$ for the Midpoint Rule.

Why it's wrong: The Midpoint Rule uses the midpoints of each subinterval, not the endpoints.

Correct: Midpoints are at $\bar{x}_i = \frac{x_{i-1} + x_i}{2}$, or equivalently at $a + \frac{\Delta x}{2}, a + \frac{3\Delta x}{2}, \ldots$

❌ Mistake: Wrong coefficients in Trapezoidal Rule

Wrong: $T_n = \Delta x[f(x_0) + f(x_1) + \cdots + f(x_n)]$

Why it's wrong: This counts interior points twice (once for each adjacent trapezoid), so you must average by using $\frac{\Delta x}{2}$ and doubling interior terms.

Correct: $T_n = \frac{\Delta x}{2}[f(x_0) + 2f(x_1) + \cdots + 2f(x_{n-1}) + f(x_n)]$

❌ Mistake: Using odd $n$ for Simpson's Rule

Wrong: Applying Simpson's Rule with $n = 5$ subintervals.

Why it's wrong: Simpson's Rule fits parabolas through consecutive triples of points, which requires pairs of subintervals. So $n$ must be even.

Correct: Use $n = 4, 6, 8, \ldots$ for Simpson's Rule.

❌ Mistake: Confusing relative and percentage error

Wrong: Saying "the relative error is 3.125%"

Why it's wrong: Relative error is a decimal (like 0.03125). Percentage error is relative error × 100.

Correct: Relative error = 0.03125, Percentage error = 3.125%

Formulas & Reference

Midpoint Rule

M_n = \Delta x \left[f(\bar{x}_1) + f(\bar{x}_2) + \cdots + f(\bar{x}_n)\right]

Approximates the integral using rectangles with heights at the midpoint of each subinterval.

Variables:

$M_n$:: midpoint approximation with n subintervals
$Δx$:: (b - a)/n, the width of each subinterval
$x̄_i$:: midpoint of the i-th subinterval

Trapezoidal Rule

T_n = \frac{\Delta x}{2}\left[f(x_0) + 2f(x_1) + 2f(x_2) + \cdots + 2f(x_{n-1}) + f(x_n)\right]

Approximates the integral using trapezoids. Coefficients are 1, 2, 2, ..., 2, 1.

Variables:

$T_n$:: trapezoidal approximation with n subintervals
$Δx$:: (b - a)/n, the width of each subinterval
$x_i$:: the i-th endpoint, x_i = a + iΔx

Simpson's Rule

S_n = \frac{\Delta x}{3}\left[f(x_0) + 4f(x_1) + 2f(x_2) + 4f(x_3) + \cdots + 4f(x_{n-1}) + f(x_n)\right]

Approximates the integral using parabolic arcs. Requires n to be even. Coefficients alternate 1, 4, 2, 4, 2, ..., 4, 1.

Variables:

$S_n$:: Simpson's approximation with n subintervals
$Δx$:: (b - a)/n, the width of each subinterval
$n$:: must be even

Absolute Error

|A - \alpha|

The absolute difference between the true value A and the approximation α.

Variables:

$A$:: true (exact) value
$α$:: approximation

Relative Error

\frac{|A - \alpha|}{|A|}

The absolute error divided by the true value. Expresses error as a fraction of the true value.

Variables:

$A$:: true (exact) value
$α$:: approximation

Percentage Error

100 \times \frac{|A - \alpha|}{|A|}\%

The relative error expressed as a percentage.

Variables:

$A$:: true (exact) value
$α$:: approximation

Courses Using This Skill

This skill is taught in the following courses. Create an account to access practice exercises and full course materials.

MATH 101 A

University of British Columbia

View Course