Volumes of Solids of Revolution / Method of Cylinders for MATH 141
Exam Relevance for MATH 141
Shell method is tested frequently in MATH 141, often alongside washers. Know when shells give an easier setup.
This skill appears on:
Understanding the Method of Cylindrical Shells
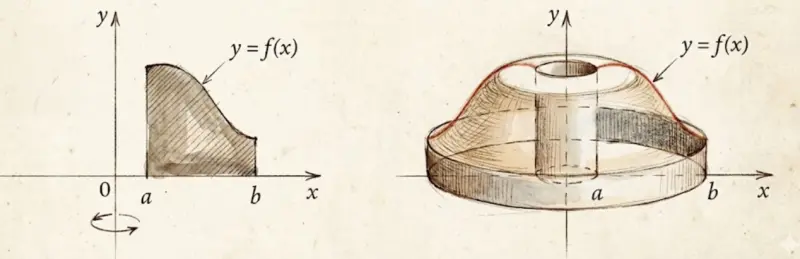
The disk/washer method slices perpendicular to the axis of rotation. But sometimes that's awkward — especially when rotating around the y-axis but the function is easier to express as $y = f(x)$.
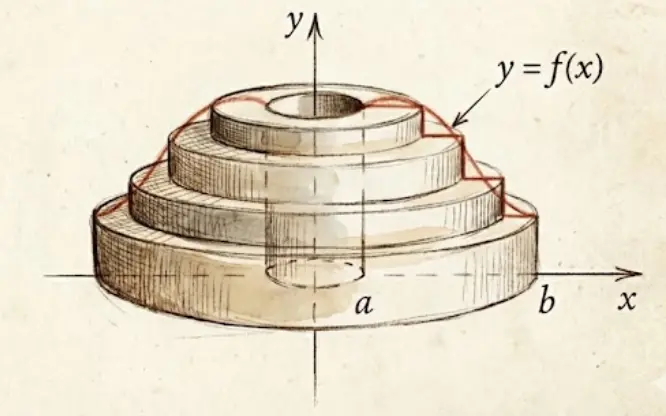
The shell method offers an alternative: instead of slicing into disks, we wrap the region into cylindrical shells (like nested tubes or cans).
The Shell Method Formula
When rotating a region around the y-axis:
$$V = \int_a^b 2\pi x \cdot f(x) \, dx$$
Where does this come from?
Each thin vertical strip at position $x$ with height $f(x)$ and thickness $dx$ becomes a cylindrical shell when rotated:
- Radius = $x$ (distance from the y-axis)
- Height = $f(x)$
- Thickness = $dx$
If you "unroll" the shell, you get a thin rectangular slab:
- Length = circumference = $2\pi x$
- Height = $f(x)$
- Thickness = $dx$
Volume of shell = $2\pi x \cdot f(x) \cdot dx$
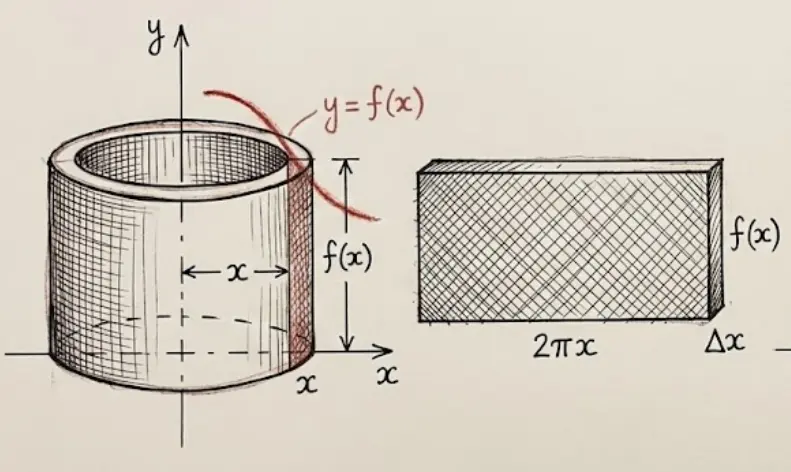
Getting the volume of a 'shell'

Problem: Find the volume when the region under $y = x^2$ from $x = 0$ to $x = 2$ is rotated around the y-axis.
$$V = \int_0^2 2\pi x \cdot x^2 \, dx = 2\pi \int_0^2 x^3 \, dx$$
$$= 2\pi \left[\frac{x^4}{4}\right]_0^2$$
$$= 2\pi \cdot \frac{16}{4} = 2\pi \cdot 4 = 8\pi$$
$$\boxed{V = 8\pi}$$
Problem: Find the volume when $y = \sqrt{x}$ from $x = 0$ to $x = 4$ is rotated around the y-axis.
$$V = \int_0^4 2\pi x \cdot \sqrt{x} \, dx = 2\pi \int_0^4 x^{3/2} \, dx$$
$$= 2\pi \left[\frac{2}{5}x^{5/2}\right]_0^4$$
$$= 2\pi \cdot \frac{2}{5} \cdot 32 = \frac{128\pi}{5}$$
$$\boxed{V = \frac{128\pi}{5}}$$
With the disk method, you'd need to rewrite as $x = y^2$ and integrate with respect to $y$ — shells are simpler here!
Shells Around the x-axis
When rotating around the x-axis, use horizontal shells:
$$V = \int_c^d 2\pi y \cdot g(y) \, dy$$
where $x = g(y)$ is the width of the shell at height $y$.
Problem: Find the volume when the region bounded by $y = x^2$, $y = 0$, and $x = 1$ is rotated around the x-axis.
Step 1: Express as x = g(y)
From $y = x^2$: $x = \sqrt{y}$
The region goes from $y = 0$ to $y = 1$.
Step 2: Find the shell width
At height $y$, the horizontal strip goes from $x = \sqrt{y}$ to $x = 1$.
Width = $1 - \sqrt{y}$
Step 3: Set up and evaluate
$$V = \int_0^1 2\pi y (1 - \sqrt{y}) \, dy$$
$$= 2\pi \int_0^1 (y - y^{3/2}) \, dy$$
$$= 2\pi \left[\frac{y^2}{2} - \frac{2}{5}y^{5/2}\right]_0^1$$
$$= 2\pi \left(\frac{1}{2} - \frac{2}{5}\right) = 2\pi \cdot \frac{1}{10} = \frac{\pi}{5}$$
$$\boxed{V = \frac{\pi}{5}}$$
Shells with Non-Axis Rotation
When rotating around a vertical line $x = h$:
$$V = \int_a^b 2\pi |x - h| \cdot f(x) \, dx$$
The radius is the distance from the strip to the axis of rotation.
Problem: Find the volume when $y = x^2$ from $x = 0$ to $x = 2$ is rotated around $x = 3$.
Step 1: Find the radius
Distance from $x$ to the line $x = 3$: radius = $3 - x$
Step 2: Set up and evaluate
$$V = \int_0^2 2\pi (3 - x) \cdot x^2 \, dx$$
$$= 2\pi \int_0^2 (3x^2 - x^3) \, dx$$
$$= 2\pi \left[x^3 - \frac{x^4}{4}\right]_0^2$$
$$= 2\pi \left(8 - 4\right) = 2\pi \cdot 4 = 8\pi$$
$$\boxed{V = 8\pi}$$
Problem: Find the volume when the region between $y = x$ and $y = x^2$ is rotated around the y-axis.
Step 1: Find intersection points
$x = x^2$ gives $x = 0$ and $x = 1$.
Step 2: Find the height of each shell
Height = (top) − (bottom) = $x - x^2$
Step 3: Set up and evaluate
$$V = \int_0^1 2\pi x (x - x^2) \, dx$$
$$= 2\pi \int_0^1 (x^2 - x^3) \, dx$$
$$= 2\pi \left[\frac{x^3}{3} - \frac{x^4}{4}\right]_0^1$$
$$= 2\pi \left(\frac{1}{3} - \frac{1}{4}\right) = 2\pi \cdot \frac{1}{12} = \frac{\pi}{6}$$
$$\boxed{V = \frac{\pi}{6}}$$
When to Use Shells vs. Disks/Washers
| Situation | Preferred Method |
|---|---|
| Rotating around y-axis, function is $y = f(x)$ | Shells |
| Rotating around x-axis, function is $x = g(y)$ | Shells |
| Rotating around x-axis, function is $y = f(x)$ | Disks/Washers |
| Rotating around y-axis, function is $x = g(y)$ | Disks/Washers |
| One method requires multiple integrals | Try the other method |
Rule of thumb: If you'd need to solve for the other variable or split into multiple integrals, try switching methods!
Common Mistakes and Misunderstandings
❌ Mistake: Forgetting the $2\pi$ factor
Wrong: $V = \int x \cdot f(x) \, dx$
Why it's wrong: The circumference of each shell is $2\pi r$, not just $r$.
Correct: $V = \int 2\pi x \cdot f(x) \, dx$
❌ Mistake: Using the wrong radius
Wrong: Using $f(x)$ as the radius when rotating around the y-axis.
Why it's wrong: The radius is the distance from the strip to the axis, which is $x$ (not the height of the function).
Correct: For rotation around the y-axis, radius = $x$. For rotation around $x = h$, radius = $|x - h|$.
❌ Mistake: Confusing shell height with shell radius
Wrong: Setting up $V = \int 2\pi f(x) \cdot x \, dx$ with $f(x)$ as radius and $x$ as height.
Why it's wrong: For shells around the y-axis: radius = $x$ (distance to axis), height = $f(x)$ (vertical extent).
Correct: Always identify: What's the distance to the axis? (radius) What's the extent parallel to the axis? (height)
❌ Mistake: Using shells when disks are simpler
Wrong: Forcing the shell method when the disk method would be straightforward.
Why it's wrong: Both methods give the same answer, but one is often much easier. Choose wisely!
Correct: If rotating around the x-axis and $y = f(x)$ is simple, use disks. If rotating around the y-axis and $y = f(x)$ is simple, use shells.
Shell Method (Rotation about y-axis)
Volume when rotating around the y-axis using cylindrical shells. Each shell has radius x, height f(x), and circumference 2πx.
Variables:
- $V$:
- volume of the solid
- $x$:
- radius of the shell (distance to y-axis)
- $f(x)$:
- height of the shell
- $a, b$:
- bounds on the x-axis
Shell Method (Rotation about x-axis)
Volume when rotating around the x-axis using cylindrical shells. Each shell has radius y, width g(y), and circumference 2πy.
Variables:
- $V$:
- volume of the solid
- $y$:
- radius of the shell (distance to x-axis)
- $g(y)$:
- width of the shell (horizontal extent)
- $c, d$:
- bounds on the y-axis
Shell Method (General Axis x = h)
Volume when rotating around a vertical line x = h. The radius is the distance from x to the axis of rotation.
Variables:
- $V$:
- volume of the solid
- $|x - h|$:
- radius (distance from x to axis x = h)
- $f(x)$:
- height of the shell
- $h$:
- the vertical line of rotation
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.