Surface Area for MATH 141
Exam Relevance for MATH 141
Surface area of revolution appears occasionally in MATH 141. Similar setup to arc length.
This skill appears on:
Understanding Surface Area of Revolution
You've learned how to find the length of a curve (arc length). Now, what if you rotate that curve around an axis? You get a 3D surface — like a vase, a funnel, or a trumpet.
The surface area of revolution formula lets you calculate the area of these curved surfaces. It's similar to arc length, but we're now wrapping the curve around to form a surface.
The Formulas
Rotation around the x-axis
For $y = f(x)$ rotated around the x-axis from $x = a$ to $x = b$:
$$S = \int_a^b 2\pi y \sqrt{1 + \left(\frac{dy}{dx}\right)^2} \, dx$$
Or equivalently:
$$S = \int_a^b 2\pi f(x) \sqrt{1 + [f'(x)]^2} \, dx$$
Rotation around the y-axis
For $x = g(y)$ rotated around the y-axis from $y = c$ to $y = d$:
$$S = \int_c^d 2\pi x \sqrt{1 + \left(\frac{dx}{dy}\right)^2} \, dy$$
Where Does This Come From?
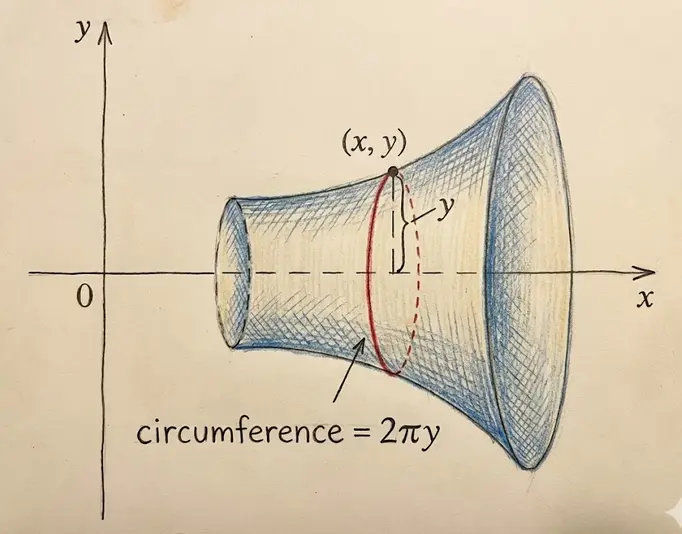
Key insight: Surface area = (circumference) × (arc length)
When you rotate a small piece of curve $ds$ around an axis:
- It traces out a "band" (like a ring)
- The band has circumference $2\pi r$ (where $r$ is the distance to the axis)
- The band has width $ds$ (the arc length element)
So each tiny band has area:
$$dS = 2\pi r \cdot ds$$
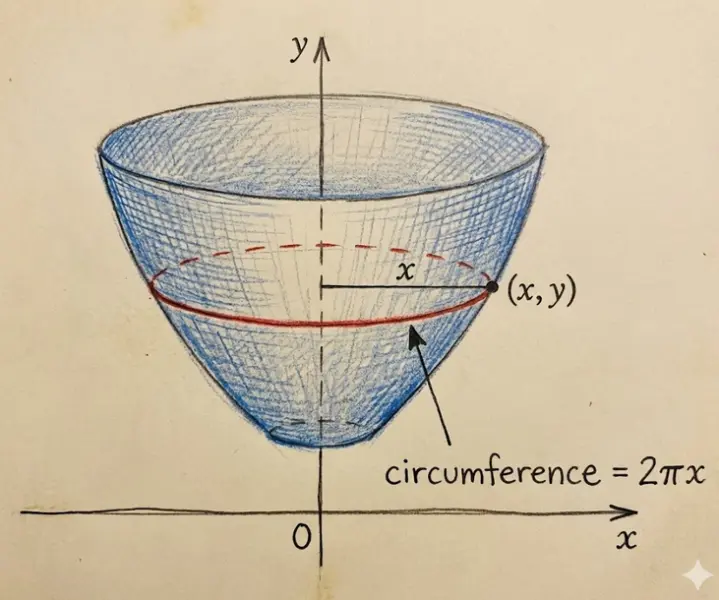
For rotation around the x-axis, $r = y$ and $ds = \sqrt{1 + (dy/dx)^2}\,dx$.
Problem: Find the surface area generated by rotating $y = x$ from $x = 0$ to $x = 2$ around the x-axis.
This creates a cone!
$\frac{dy}{dx} = 1$
$$S = \int_0^2 2\pi x \sqrt{1 + 1^2} \, dx$$
$$= \int_0^2 2\pi x \sqrt{2} \, dx$$
$$= 2\pi\sqrt{2} \int_0^2 x \, dx$$
$$= 2\pi\sqrt{2} \left[\frac{x^2}{2}\right]_0^2$$
$$= 2\pi\sqrt{2} \cdot 2 = 4\pi\sqrt{2}$$
$$\boxed{S = 4\pi\sqrt{2} \approx 17.77}$$
Problem: Find the surface area of a sphere of radius $r$ by rotating $y = \sqrt{r^2 - x^2}$ (upper semicircle) around the x-axis.
First, find $\frac{dy}{dx}$:
$$y = \sqrt{r^2 - x^2} = (r^2 - x^2)^{1/2}$$
$$\frac{dy}{dx} = \frac{-x}{\sqrt{r^2 - x^2}}$$
Now compute $1 + \left(\frac{dy}{dx}\right)^2$:
$$1 + \frac{x^2}{r^2 - x^2} = \frac{r^2 - x^2 + x^2}{r^2 - x^2} = \frac{r^2}{r^2 - x^2}$$
Take the square root:
$$\sqrt{1 + \left(\frac{dy}{dx}\right)^2} = \frac{r}{\sqrt{r^2 - x^2}}$$
Set up the integral from $x = -r$ to $x = r$:
$$S = \int_{-r}^{r} 2\pi \sqrt{r^2 - x^2} \cdot \frac{r}{\sqrt{r^2 - x^2}} \, dx$$
The $\sqrt{r^2 - x^2}$ terms cancel!
$$= \int_{-r}^{r} 2\pi r \, dx = 2\pi r [x]_{-r}^{r}$$
$$= 2\pi r (r - (-r)) = 2\pi r (2r)$$
$$\boxed{S = 4\pi r^2}$$
This is the famous sphere surface area formula!
Problem: Find the surface area generated by rotating $y = x^2$ from $x = 0$ to $x = 1$ around the y-axis.
Step 1: Rewrite as x = g(y)
Since $y = x^2$ and $x \geq 0$, we have $x = \sqrt{y}$.
When $x = 0$: $y = 0$. When $x = 1$: $y = 1$.
Step 2: Find the derivative
$$\frac{dx}{dy} = \frac{1}{2\sqrt{y}}$$
Step 3: Set up the integral
$$S = \int_0^1 2\pi x \sqrt{1 + \left(\frac{dx}{dy}\right)^2} \, dy$$
$$= \int_0^1 2\pi \sqrt{y} \sqrt{1 + \frac{1}{4y}} \, dy$$
$$= \int_0^1 2\pi \sqrt{y} \cdot \sqrt{\frac{4y + 1}{4y}} \, dy$$
$$= \int_0^1 2\pi \sqrt{y} \cdot \frac{\sqrt{4y + 1}}{2\sqrt{y}} \, dy$$
$$= \pi \int_0^1 \sqrt{4y + 1} \, dy$$
Step 4: Evaluate
Let $u = 4y + 1$, so $du = 4\,dy$.
When $y = 0$: $u = 1$. When $y = 1$: $u = 5$.
$$= \frac{\pi}{4} \int_1^5 \sqrt{u} \, du$$
$$= \frac{\pi}{4} \cdot \frac{2}{3} u^{3/2} \Big|_1^5$$
$$= \frac{\pi}{6} (5^{3/2} - 1)$$
$$= \frac{\pi}{6} (5\sqrt{5} - 1)$$
$$\boxed{S = \frac{\pi(5\sqrt{5} - 1)}{6} \approx 5.33}$$
Parametric Surface Area
For a parametric curve $x = x(t)$, $y = y(t)$ rotated around the x-axis:
$$S = \int_a^b 2\pi y \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} \, dt$$
Problem: Find the surface area generated by rotating $x = \cos t$, $y = \sin t$ from $t = 0$ to $t = \frac{\pi}{2}$ around the x-axis.
$$\frac{dx}{dt} = -\sin t, \quad \frac{dy}{dt} = \cos t$$
$$\sqrt{\sin^2 t + \cos^2 t} = 1$$
$$S = \int_0^{\pi/2} 2\pi \sin t \cdot 1 \, dt$$
$$= 2\pi [-\cos t]_0^{\pi/2}$$
$$= 2\pi (0 - (-1)) = 2\pi$$
$$\boxed{S = 2\pi}$$
This is the surface area of a hemisphere of radius 1 (half of $4\pi r^2 = 4\pi$).
Common Mistakes and Misunderstandings
❌ Mistake: Using the wrong radius
Wrong: Always using $y$ as the radius regardless of the axis of rotation.
Why it's wrong: The radius is the distance from the curve to the axis of rotation.
- Rotating around x-axis: radius = $y$ (vertical distance)
- Rotating around y-axis: radius = $x$ (horizontal distance)
Correct: Identify which axis you're rotating around, then use the appropriate coordinate as the radius.
❌ Mistake: Forgetting the $2\pi$ factor
Wrong: $S = \int y \sqrt{1 + (dy/dx)^2} \, dx$
Why it's wrong: You're missing the circumference factor. Each arc length element traces a circle when rotated.
Correct: $S = \int 2\pi y \sqrt{1 + (dy/dx)^2} \, dx$
❌ Mistake: Confusing surface area with arc length
Wrong: Using $S = \int \sqrt{1 + (f')^2} \, dx$ for surface area.
Why it's wrong: That's the arc length formula! Surface area needs the extra $2\pi r$ factor.
Correct:
- Arc length: $L = \int \sqrt{1 + (f')^2} \, dx$
- Surface area: $S = \int 2\pi r \sqrt{1 + (f')^2} \, dx$
❌ Mistake: Using the wrong limits when switching variables
Wrong: Keeping x-limits when integrating with respect to y.
Why it's wrong: When you change from $y = f(x)$ to $x = g(y)$, you must also convert the bounds!
Correct: If $y = x^2$ from $x = 0$ to $x = 2$, then $x = \sqrt{y}$ from $y = 0$ to $y = 4$.
Surface Area (Rotation about x-axis)
Surface area when y = f(x) is rotated around the x-axis. The radius is y (distance to x-axis).
Variables:
- $S$:
- surface area
- $y$:
- function value (radius of rotation)
- $a, b$:
- x-bounds of the curve
- $dy/dx$:
- derivative of the curve
Surface Area (Rotation about y-axis)
Surface area when x = g(y) is rotated around the y-axis. The radius is x (distance to y-axis).
Variables:
- $S$:
- surface area
- $x$:
- function value (radius of rotation)
- $c, d$:
- y-bounds of the curve
- $dx/dy$:
- derivative of the curve
Surface Area (Parametric, about x-axis)
Surface area when a parametric curve is rotated around the x-axis.
Variables:
- $S$:
- surface area
- $y$:
- y-coordinate (radius of rotation)
- $a, b$:
- parameter bounds
- $dx/dt, dy/dt$:
- derivatives with respect to parameter
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.