Alternating Series Test for MATH 141
Exam Relevance for MATH 141
AST appears on MATH 141 finals. Also know the error bound: |error| <= first omitted term.
This skill appears on:
Understanding the Alternating Series Test
So far, all our convergence tests have required positive terms. But what about series that alternate between positive and negative? The Alternating Series Test gives us a surprisingly simple way to determine convergence for these series — and often, series that would diverge with all positive terms will converge once you add alternating signs.
What is an Alternating Series?
An alternating series has terms that flip between positive and negative:
$$\sum_{n=1}^{\infty} (-1)^{n+1} b_n = b_1 - b_2 + b_3 - b_4 + \cdots$$
$$\sum_{n=1}^{\infty} (-1)^{n} b_n = -b_1 + b_2 - b_3 + b_4 - \cdots$$
where $b_n > 0$ for all $n$.
Classic examples:
- $\displaystyle 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots$ (alternating harmonic)
- $\displaystyle -1 + \frac{1}{4} - \frac{1}{9} + \frac{1}{16} - \cdots$
The Test (Two Conditions)
The alternating series $\displaystyle\sum_{n=1}^{\infty} (-1)^{n+1} b_n$ converges if:
Condition 1: $b_{n+1} \leq b_n$ for all $n$ (decreasing)
Condition 2: $\displaystyle\lim_{n \to \infty} b_n = 0$
Both conditions must be satisfied!
Why Does This Work?
The partial sums $S_n$ "bounce" back and forth on the number line, getting closer to the limit $S$ with each term.
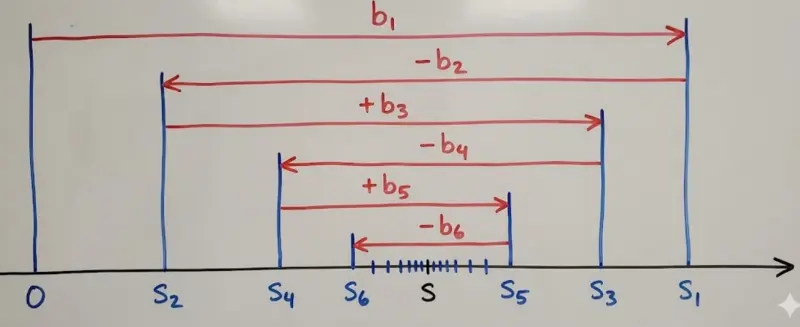
Starting from 0, add $b_1$ to get $S_1$. Then subtract $b_2$ to get $S_2$. Then add $b_3$ to get $S_3$, and so on. Each step moves you back and forth: $S_1$, $S_3$, $S_5$, ... approach $S$ from the right while $S_2$, $S_4$, $S_6$, ... approach from the left. Because the $b_n$ are decreasing toward zero, the bounces get smaller, trapping $S$ in an ever-shrinking interval.
Visualizing Terms and Partial Sums
This shows both the terms $a_n = (-1)^{n+1}b_n$ and partial sums $S_n$ plotted against $n$:
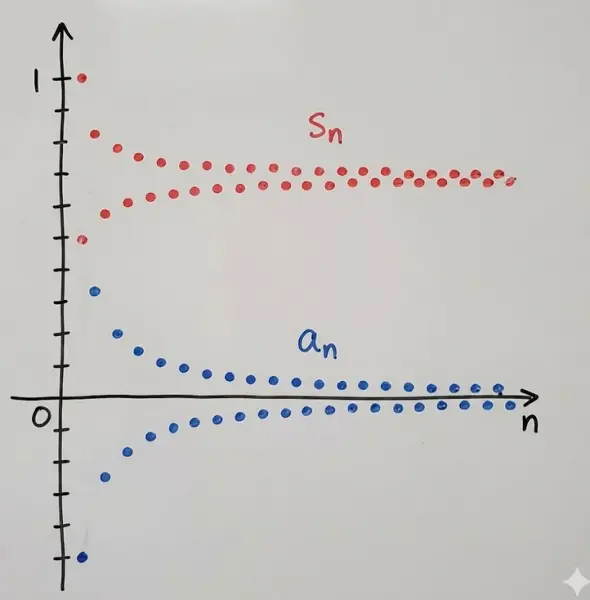
The blue dots show the terms $a_n$ alternating above and below zero, with magnitudes shrinking toward zero. The red dots show the partial sums $S_n$ oscillating but converging toward the series sum. Odd partial sums approach from above; even partial sums approach from below.
Does $\displaystyle\sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots$ converge?
Here $b_n = \frac{1}{n}$.
Check condition 1: Is $b_{n+1} \leq b_n$? $$\frac{1}{n+1} \leq \frac{1}{n} \quad \checkmark$$
Check condition 2: Is $\lim_{n \to \infty} b_n = 0$? $$\lim_{n \to \infty} \frac{1}{n} = 0 \quad \checkmark$$
Both conditions satisfied → Converges.
Key insight: The regular harmonic series $\sum \frac{1}{n}$ diverges, but alternating signs make it converge! (Converges to $\ln 2$.)
Does $\displaystyle\sum_{n=1}^{\infty} \frac{(-1)^{n}}{n^{1/3}}$ converge?
Here $b_n = \frac{1}{n^{1/3}}$.
Check condition 1: $\frac{1}{(n+1)^{1/3}} \leq \frac{1}{n^{1/3}}$ $\checkmark$
Check condition 2: $\lim_{n \to \infty} \frac{1}{n^{1/3}} = 0$ $\checkmark$
Both satisfied → Converges.
Note: The non-alternating $\sum \frac{1}{n^{1/3}}$ diverges ($p = 1/3 < 1$).
Does $\displaystyle\sum_{n=1}^{\infty} (-1)^{n+1} \frac{n}{2n+1}$ converge?
Here $b_n = \frac{n}{2n+1}$.
Check condition 2: Is $\lim_{n \to \infty} b_n = 0$? $$\lim_{n \to \infty} \frac{n}{2n+1} = \frac{1}{2} \neq 0$$
Condition 2 fails → Alternating Series Test does not apply.
Since $\lim_{n \to \infty} a_n \neq 0$, by the Divergence Test, this series diverges.
Does $\displaystyle\sum_{n=1}^{\infty} (-1)^{n+1} \frac{n}{n^2 + 1}$ converge?
Here $b_n = \frac{n}{n^2 + 1}$.
Check condition 2: $$\lim_{n \to \infty} \frac{n}{n^2 + 1} = \lim_{n \to \infty} \frac{1}{n + \frac{1}{n}} = 0 \quad \checkmark$$
Check condition 1: Show $f(x) = \frac{x}{x^2 + 1}$ is decreasing.
$$f'(x) = \frac{(x^2+1) - x(2x)}{(x^2+1)^2} = \frac{1 - x^2}{(x^2+1)^2}$$
For $x > 1$: $f'(x) < 0$ → decreasing $\checkmark$
Both conditions satisfied → Converges.
Does $\displaystyle\sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n!}$ converge?
Here $b_n = \frac{1}{n!}$.
Check condition 1: $$\frac{1}{(n+1)!} = \frac{1}{(n+1) \cdot n!} < \frac{1}{n!} \quad \checkmark$$
Check condition 2: $\lim_{n \to \infty} \frac{1}{n!} = 0$ $\checkmark$
Both satisfied → Converges.
The Alternating Series Estimation Theorem
If an alternating series satisfies both conditions of the test, then:
$$|S - S_n| \leq b_{n+1}$$
The error in approximating $S$ with $S_n$ is at most the first omitted term.
For the alternating harmonic series, how accurate is $S_4$ as an approximation?
We have $S_4 = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} = \frac{7}{12} \approx 0.583$.
By the Estimation Theorem: $$|S - S_4| \leq b_5 = \frac{1}{5} = 0.2$$
So $S_4$ is within $0.2$ of the true sum.
The actual sum is $\ln 2 \approx 0.693$, and indeed $|0.693 - 0.583| = 0.11 < 0.2$ $\checkmark$
Absolute vs Conditional Convergence
| Type | Definition | Example |
|---|---|---|
| Absolutely convergent | $\sum |a_n|$ converges | $\sum \frac{(-1)^n}{n^2}$ |
| Conditionally convergent | $\sum a_n$ converges but $\sum |a_n|$ diverges | $\sum \frac{(-1)^{n+1}}{n}$ |
The alternating harmonic series is conditionally convergent: it converges, but its absolute value (the harmonic series) diverges.
Common Mistakes and Misunderstandings
❌ Mistake: Forgetting to check both conditions
Wrong: "The terms go to zero, so it converges."
Why it's wrong: Both conditions are required. Terms must decrease AND approach zero.
Correct: Always verify $b_{n+1} \leq b_n$ AND $\lim b_n = 0$.
❌ Mistake: Confusing $a_n$ and $b_n$
Wrong: Working with $a_n = \frac{(-1)^{n+1}}{n}$ directly when checking conditions.
Why it's wrong: The conditions apply to $b_n = |a_n|$, the positive part.
Correct: Extract $b_n$ first: if $a_n = \frac{(-1)^{n+1}}{n}$, then $b_n = \frac{1}{n}$.
❌ Mistake: Assuming alternating = converges
Wrong: "It alternates, so it must converge."
Why it's wrong: Not all alternating series converge! See Example 3.
Correct: Apply the test — both conditions must hold.
The Alternating Series Test
Both conditions must be satisfied: the terms must be decreasing AND approach zero.
Variables:
- $b_n$:
- the positive part of the terms (b_n > 0)
- $(-1)^{n+1}$:
- creates the alternating signs
Alternating Series Estimation Theorem
The error in approximating the sum S with partial sum S_n is at most the absolute value of the first omitted term.
Variables:
- $S$:
- the true sum of the series
- $S_n$:
- the partial sum of the first n terms
- $b_{n+1}$:
- the (n+1)th term in absolute value
Absolute vs Conditional Convergence
The alternating harmonic series is conditionally convergent — it converges, but the harmonic series (its absolute value) diverges.
Variables:
- $a_n$:
- the terms of the series (including signs)
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.