Newton’s Method for MATH 140

What is Newton's Method?

Newton's Method (also called Newton-Raphson) is a technique for finding roots of equations — that is, finding where $f(x) = 0$.

Isaac Newton developed this iterative approach: start with a guess, then repeatedly improve it using calculus until you're close enough to the actual root.

The Big Idea: Use the tangent line at your current guess to find a better guess. Repeat until you converge to the root.

Why Do We Need This?

Some equations can't be solved algebraically. For example:

• $x^5 - x - 1 = 0$ — no formula exists for 5th-degree polynomials!
• $\cos(x) = x$ — mixing trig and polynomials
• $e^x = 3x$ — mixing exponentials and polynomials

Newton's Method gives us a way to find approximate solutions to any precision we want.

The Formula

Starting from an initial guess $x_0$, each new approximation is:

$$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$$

What This Means

1. Evaluate $f(x_n)$ — how far is your current guess from being a root?
2. Evaluate $f'(x_n)$ — what's the slope of the tangent line there?
3. Compute the ratio and subtract — this gives you the next (better) guess

Key Variables

• $x_n$ — your current approximation (the $n$-th guess)
• $x_{n+1}$ — your next approximation (hopefully closer to the root)
• $f(x_n)$ — the function value at your current guess
• $f'(x_n)$ — the derivative (slope) at your current guess

The Geometric Intuition

Here's what's actually happening:

1. You're at a point $(x_n, f(x_n))$ on the curve
2. Draw the tangent line at that point
3. Find where the tangent line crosses the x-axis
4. That x-intercept becomes your new guess $x_{n+1}$

The tangent line is a good local approximation of the curve, so its root is close to the curve's root!

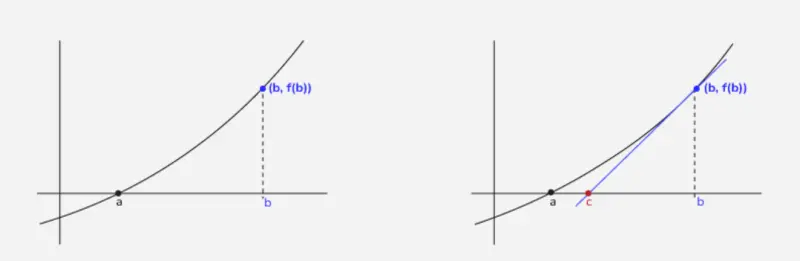
Starting from $x_0 = b$, watch how each tangent line leads us closer to the root $a$.

When Newton's Method Fails

Newton's Method doesn't always work! Watch out for:

1. Bad starting point — if $x_0$ is too far from the root, you might converge to a different root or not converge at all

2. Derivative is zero — if $f'(x_n) = 0$, you're dividing by zero!

3. Oscillation — sometimes the method bounces back and forth without converging

4. Divergence — the approximations can get further from the root instead of closer

Pro tip: Choose $x_0$ by sketching the graph or using a calculator to find roughly where the function crosses zero.

Tips for Newton's Method Problems

1. Always find $f'(x)$ first — you'll need it for every iteration
2. Set up the iteration formula before plugging in numbers
3. Keep track of your iterations — organize as $x_0, x_1, x_2, ...$
4. Watch for convergence — when successive values agree to the required decimal places, you're done
5. Use a calculator — the arithmetic can get messy, and that's okay!

Common Mistakes and Misunderstandings

❌ Mistake: Forgetting the minus sign

Wrong: $x_{n+1} = x_n + \frac{f(x_n)}{f'(x_n)}$

Why it's wrong: The formula has a subtraction, not addition.

Correct: $x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$

❌ Mistake: Not rewriting the equation as $f(x) = 0$

Wrong: Using $f(x) = \cos(x)$ when solving $\cos(x) = x$.

Why it's wrong: Newton's Method finds roots (where $f(x) = 0$). You need $f(x) = \cos(x) - x$.

Correct: Rearrange to $\cos(x) - x = 0$, then use $f(x) = \cos(x) - x$.

❌ Mistake: Using the wrong derivative

Wrong: Forgetting chain rule or making arithmetic errors with $f'(x)$.

Why it's wrong: An incorrect derivative will give you wrong iterations.

Correct: Double-check your derivative before starting iterations.