Solved Math Exams

What is the Intermediate Value Theorem?

The Intermediate Value Theorem (IVT) says that if a continuous function starts at one value and ends at another, it must hit every value in between at some point.

Intuitive idea: If you're at ground level and later you're on the 10th floor, you must have passed through floors 1, 2, 3, ... 9 at some point. You can't teleport!

The Formal Statement

Intermediate Value Theorem: If $f$ is continuous on $[a, b]$ and $N$ is any number between $f(a)$ and $f(b)$, then there exists at least one $c$ in $(a, b)$ such that $f(c) = N$.

In plain English:

You have a continuous function on an interval $[a, b]$
Pick any $y$-value $N$ between $f(a)$ and $f(b)$
The theorem guarantees there's some $x = c$ where $f(c) = N$

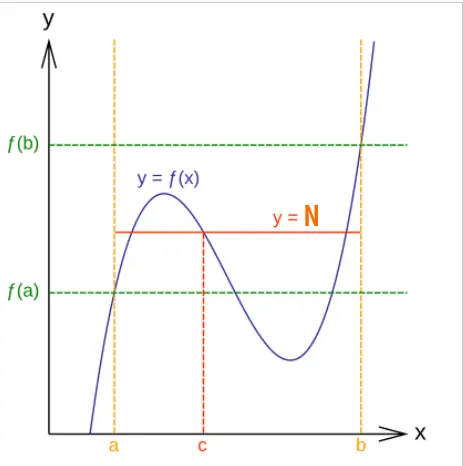
In this graph, notice how the continuous curve must cross the horizontal line $y = N$ at least once. The $x$-coordinate where this crossing happens is the value $c$ that the theorem guarantees exists.

Key Requirements

The IVT only works when both conditions are met:

Condition	Why it matters
$f$ is continuous on $[a, b]$	No jumps or holes—the function can be drawn without lifting your pen
$N$ is between $f(a)$ and $f(b)$	The target value must be in the range the function covers

⚠️ Critical: If the function has a discontinuity (jump, hole, or asymptote) in the interval, the IVT does not apply!

The Most Common Application: Proving a Root Exists

The IVT is most often used to prove that an equation $f(x) = 0$ has a solution in some interval.

Strategy:

Find an interval $[a, b]$ where $f(a)$ and $f(b)$ have opposite signs
Since $0$ is between a positive and negative number, IVT guarantees a root exists

Example 1: Proving a Root Exists

Problem: Show that $f(x) = x^3 - x - 1$ has a root in the interval $[1, 2]$.

Step 1: Verify $f$ is continuous on $[1, 2]$.

$f(x) = x^3 - x - 1$ is a polynomial, so it's continuous everywhere. ✓

Step 2: Calculate $f(a)$ and $f(b)$.

$$f(1) = 1^3 - 1 - 1 = -1 \quad \text{(negative)}$$ $$f(2) = 2^3 - 2 - 1 = 5 \quad \text{(positive)}$$

Step 3: Apply IVT.

Since $f(1) = -1 < 0 < 5 = f(2)$, and $f$ is continuous on $[1, 2]$, the IVT guarantees there exists some $c \in (1, 2)$ such that $f(c) = 0$.

$$\boxed{\text{By IVT, } f(x) = x^3 - x - 1 \text{ has at least one root in } (1, 2)}$$

Example 2: Finding an Interval That Contains a Root

Problem: Show that $e^x = 3 - x$ has a solution.

Step 1: Rewrite as $f(x) = 0$.

Let $f(x) = e^x - (3 - x) = e^x + x - 3$

We need to find where $f(x) = 0$.

Step 2: Find values where $f$ changes sign.

Try $x = 0$: $$f(0) = e^0 + 0 - 3 = 1 - 3 = -2 \quad \text{(negative)}$$

Try $x = 1$: $$f(1) = e^1 + 1 - 3 = e - 2 \approx 2.718 - 2 = 0.718 \quad \text{(positive)}$$

Step 3: Apply IVT.

Since $f$ is continuous (it's $e^x$ plus a polynomial), and $f(0) < 0 < f(1)$, by IVT there exists $c \in (0, 1)$ such that $f(c) = 0$.

$$\boxed{\text{By IVT, } e^x = 3 - x \text{ has a solution in } (0, 1)}$$

Example 3: IVT with a Specific Value (Not Zero)

Problem: Show that $f(x) = x^2$ takes the value $3$ somewhere in $[1, 2]$.

Step 1: Check continuity.

$f(x) = x^2$ is a polynomial, so it's continuous. ✓

Step 2: Calculate $f(1)$ and $f(2)$.

$$f(1) = 1 \quad \text{and} \quad f(2) = 4$$

Step 3: Is $N = 3$ between these values?

Yes! $1 < 3 < 4$ ✓

Step 4: Apply IVT.

By IVT, there exists $c \in (1, 2)$ such that $f(c) = 3$.

$$\boxed{\text{By IVT, } x^2 = 3 \text{ has a solution in } (1, 2)}$$

(We know this solution is $c = \sqrt{3} \approx 1.732$)

Example 4: When IVT Does NOT Apply

Problem: Does $f(x) = \frac{1}{x}$ have a value of $0$ in $[-1, 1]$?

Step 1: Check the conditions.

$f(-1) = -1$ and $f(1) = 1$

These have opposite signs, and $0$ is between them...

Step 2: BUT is $f$ continuous on $[-1, 1]$?

No! $f(x) = \frac{1}{x}$ has a vertical asymptote at $x = 0$. The function is discontinuous in this interval.

Conclusion: IVT does not apply. And indeed, $\frac{1}{x} = 0$ has no solution anywhere!

$$\boxed{\text{IVT cannot be applied—} f \text{ is not continuous on } [-1, 1]}$$

Common Mistakes and Misunderstandings

❌ Mistake: Applying IVT to discontinuous functions

Wrong: "Since $f(-1) = -1$ and $f(1) = 1$ for $f(x) = \frac{1}{x}$, there must be a root in $[-1, 1]$."

Why it's wrong: The IVT requires continuity on the entire interval. The discontinuity at $x = 0$ breaks the theorem's conditions.

Correct: First verify continuity, then apply IVT. If there's any discontinuity in $[a, b]$, IVT cannot be used.

❌ Mistake: Thinking IVT tells you exactly where the root is

Wrong: "By IVT, the root is at $c = 1.5$."

Why it's wrong: IVT is an existence theorem—it only tells you a root exists, not its exact value. To find the actual root, you need other methods (bisection, Newton's method, etc.).

Correct: "By IVT, a root exists in $(1, 2)$." (Don't claim to know the exact value unless you calculate it separately.)

❌ Mistake: Forgetting to check that $N$ is between $f(a)$ and $f(b)$

Wrong: Using IVT to claim $f(x) = x^2$ equals $10$ on $[0, 2]$.

Why it's wrong: $f(0) = 0$ and $f(2) = 4$, so the range is $[0, 4]$. The value $10$ is not between $0$ and $4$.

Correct: IVT only guarantees values between $f(a)$ and $f(b)$. Here, IVT can prove $f(x) = 3$ has a solution (since $0 < 3 < 4$), but not $f(x) = 10$.

Writing IVT Proofs on Exams

When asked to "use IVT to show..." follow this template:

State that $f$ is continuous on $[a, b]$ (and why—polynomial, exponential, etc.)
Calculate $f(a)$ and $f(b)$
Note that $N$ (often $0$) is between them
Conclude "By IVT, there exists $c \in (a, b)$ such that $f(c) = N$"

This structure earns full marks on most exams.

Intermediate Value Theorem for MATH 140

Exam Relevance for MATH 140

This skill appears on: