Continuity for MATH 140
Exam Relevance for MATH 140
Continuity questions appear on every MATH 140 exam. Know the three conditions and how to find values that make functions continuous.
This skill appears on:
What is Continuity?
Intuitive Definition: A function is continuous if you can draw its graph without lifting your pencil.
If you have to lift your pencil (because of a jump, hole, or asymptote), the function is discontinuous at that point.
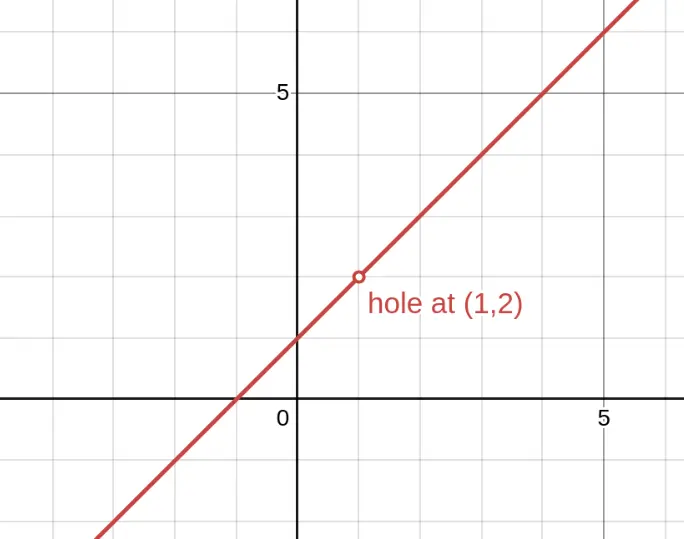
In this graph, we see $f(x) = \frac{x^2-1}{x-1}$, which looks like the line $y = x + 1$ but has a hole at the point $(1, 2)$. The function is discontinuous at $x = 1$ because $f(1)$ is undefined.
The Formal Definition
A function $f$ is continuous at $x = a$ if ALL THREE conditions are met:
| Condition | What to Check |
|---|---|
| 1. $f(a)$ exists | The function is defined at $a$ |
| 2. $\displaystyle\lim_{x \to a} f(x)$ exists | The limit exists (left = right) |
| 3. $\displaystyle\lim_{x \to a} f(x) = f(a)$ | The limit equals the function value |
Memory trick: The limit must exist, the value must exist, and they must be equal!
Types of Discontinuities
1. Removable Discontinuity (Hole)
- The limit exists, but $f(a)$ is either undefined or different from the limit
- Can be "fixed" by redefining $f(a)$
- Graph has a hole (missing point)
2. Jump Discontinuity
- The one-sided limits exist but are different
- $\displaystyle\lim_{x \to a^-} f(x) \neq \lim_{x \to a^+} f(x)$
- Common in piecewise functions
- Graph has a jump between pieces
3. Infinite Discontinuity (Asymptote)
- The limit is $\pm\infty$
- Graph has a vertical asymptote
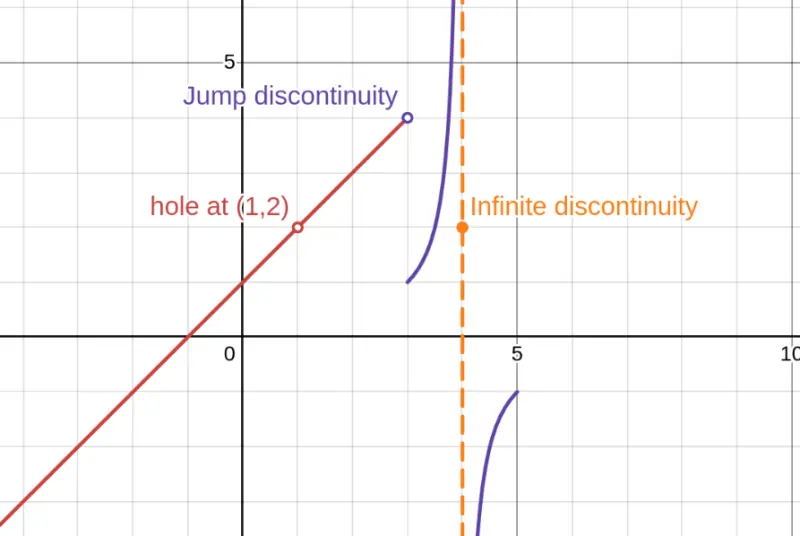
In this graph, we compare the three types: a hole (removable), a jump (piecewise function), and a vertical asymptote (infinite discontinuity).
Functions That Are Always Continuous
These functions are continuous everywhere in their domain:
| Function Type | Example | Where Continuous |
|---|---|---|
| Polynomials | $x^2 + 3x - 5$ | All real numbers |
| Exponentials | $e^x$, $2^x$ | All real numbers |
| Sine/Cosine | $\sin x$, $\cos x$ | All real numbers |
| Rational | $\frac{p(x)}{q(x)}$ | Everywhere except where $q(x) = 0$ |
| Roots | $\sqrt{x}$, $\sqrt[3]{x}$ | Their domain |
| Logarithms | $\ln x$ | $x > 0$ |
Problem: Is $f(x) = \frac{x^2 - 1}{x - 1}$ continuous at $x = 1$?
Step 1: Check if $f(1)$ exists
$$f(1) = \frac{1^2 - 1}{1 - 1} = \frac{0}{0} \quad \text{Undefined!}$$
Condition 1 fails → $f$ is NOT continuous at $x = 1$.
Step 2: Identify the type of discontinuity
Find the limit by factoring: $$\lim_{x \to 1} \frac{x^2-1}{x-1} = \lim_{x \to 1} \frac{(x-1)(x+1)}{x-1} = \lim_{x \to 1} (x+1) = 2$$
The limit exists and equals 2, so this is a removable discontinuity (hole) at the point $(1, 2)$.
Problem: Is $f(x) = \begin{cases} x^2 & \text{if } x < 2 \\ 3x - 2 & \text{if } x \geq 2 \end{cases}$ continuous at $x = 2$?
Step 1: Check all three conditions
Condition 1: Is $f(2)$ defined? $$f(2) = 3(2) - 2 = 4 \quad \checkmark$$
Condition 2: Does the limit exist?
- From the left: $\displaystyle\lim_{x \to 2^-} x^2 = 4$
- From the right: $\displaystyle\lim_{x \to 2^+} (3x-2) = 4$
- Both sides equal 4, so $\displaystyle\lim_{x \to 2} f(x) = 4 \quad \checkmark$
Condition 3: Does limit = function value? $$\lim_{x \to 2} f(x) = 4 = f(2) \quad \checkmark$$
All three conditions pass!
$$\boxed{\text{Yes, } f \text{ is continuous at } x = 2}$$
Problem: Find all discontinuities of $f(x) = \frac{x}{x^2 - 4}$
Step 1: Find where the denominator equals zero
$$x^2 - 4 = 0$$ $$(x-2)(x+2) = 0$$ $$x = 2 \text{ or } x = -2$$
Step 2: Check the numerator at these points
| $x$ value | Numerator | Denominator | Type |
|---|---|---|---|
| $x = 2$ | $2 \neq 0$ | $0$ | Infinite (asymptote) |
| $x = -2$ | $-2 \neq 0$ | $0$ | Infinite (asymptote) |
Since numerator $\neq 0$ at both points, we have $\frac{\text{non-zero}}{0} \to \pm\infty$.
$$\boxed{\text{Vertical asymptotes at } x = 2 \text{ and } x = -2}$$
Problem: Find $k$ so that $f(x) = \begin{cases} x^2 + k & \text{if } x < 1 \\ 2x & \text{if } x \geq 1 \end{cases}$ is continuous at $x = 1$.
Step 1: Set up the continuity requirement
For continuity, the left and right limits must equal each other (and equal $f(1)$): $$\lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x)$$
Step 2: Evaluate each side
- From the left: $\displaystyle\lim_{x \to 1^-} (x^2 + k) = 1^2 + k = 1 + k$
- From the right: $\displaystyle\lim_{x \to 1^+} 2x = 2(1) = 2$
Step 3: Solve for $k$
$$1 + k = 2$$ $$\boxed{k = 1}$$
Common Mistakes and Misunderstandings
❌ Mistake: Checking only ONE condition for continuity
Wrong: "The limit exists, so it's continuous."
Why it's wrong: Continuity requires ALL THREE conditions:
- $f(a)$ exists
- $\lim_{x \to a} f(x)$ exists
- They're equal
A hole has an existing limit but fails condition 1 or 3!
Correct: Always check all three conditions.
❌ Mistake: Confusing "continuous" with "differentiable"
Wrong: "The function is continuous, so I can take its derivative everywhere."
Why it's wrong: Continuity does NOT guarantee differentiability. A function can be continuous but have a sharp corner (like $|x|$ at $x = 0$) where the derivative doesn't exist.
Correct: Differentiable → Continuous (always true), but Continuous → Differentiable (NOT always true).
❌ Mistake: Forgetting to check one-sided limits for piecewise functions
Wrong: Just plugging in $x = a$ into one piece of the function.
Why it's wrong: At the boundary of a piecewise function, you must check BOTH sides approach the same value.
Correct: Always compute $\lim_{x \to a^-}$ and $\lim_{x \to a^+}$ separately, then verify they're equal.
❌ Mistake: Thinking a hole means the limit doesn't exist
Wrong: "$f(x) = \frac{x^2-1}{x-1}$ has a hole at $x=1$, so the limit doesn't exist."
Why it's wrong: A hole means the FUNCTION is undefined, but the LIMIT still exists! The limit is just the y-coordinate of the hole.
Correct: $\displaystyle\lim_{x \to 1} \frac{x^2-1}{x-1} = 2$ (the limit exists, it's the function value that doesn't).
❌ Mistake: Assuming rational functions are always discontinuous
Wrong: "This is a fraction, so it must have discontinuities."
Why it's wrong: Rational functions are continuous everywhere IN THEIR DOMAIN. They're only discontinuous where the denominator equals zero.
Correct: $f(x) = \frac{x^2 + 1}{x^2 + 4}$ is continuous everywhere (denominator is never zero).
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.