The Definition of the Derivative for MATH 139
Exam Relevance for MATH 139
Expect at least one limit definition problem. Know both forms. Show all steps.
⚠️ This Section is THE Foundation of Calculus
Most first-year calculus courses are built entirely around understanding derivatives. The notation, the geometry, the limit definition — everything in this section forms the foundation for the entire course. If there's one topic to master completely, it's this one. Take your time here. Every concept that follows (derivative rules, applications, optimization, related rates) assumes you deeply understand what's happening in this section.
What is a Derivative?
Imagine you're driving a car. Your speedometer tells you how fast you're going right now — not your average speed over the trip, but your exact speed at this instant.
That's what a derivative does for any function: it tells you the instantaneous rate of change.
Formal Definition: The derivative of $f(x)$ at a point tells you how fast $f$ is changing at that exact point.
| If you know... | The derivative tells you... |
|---|---|
| Position $s(t)$ | Velocity $s'(t)$ — how fast position changes |
| Velocity $v(t)$ | Acceleration $v'(t)$ — how fast velocity changes |
| Revenue $R(x)$ | Marginal revenue $R'(x)$ — extra revenue per unit |
| Cost $C(x)$ | Marginal cost $C'(x)$ — extra cost per unit |
The Two Limit Definitions
Both forms below are equivalent. Your course may prefer one over the other, so practice both. Know when to use each.
Form 1: The "$h$-form" (most common)
$$f'(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h}$$
- Think of $h$ as a tiny step away from $a$
- You're measuring slope between $a$ and $a + h$
- Use this when: finding a general derivative formula $f'(x)$
Form 2: The "$x \to a$ form" (alternate)
$$f'(a) = \lim_{x \to a} \frac{f(x) - f(a)}{x - a}$$
- Think of $x$ sliding toward $a$
- You're measuring slope between a moving point $x$ and fixed point $a$
- Use this when: given specific function values or finding derivative at one point
What Does This Formula Mean?
The expression $\dfrac{f(a+h) - f(a)}{h}$ is the slope of a secant line connecting two points:
- Point 1: $(a, f(a))$
- Point 2: $(a+h, f(a+h))$
As $h \to 0$, the second point slides toward the first, and the secant line becomes the tangent line.
$$\boxed{\text{Derivative} = \text{Slope of the tangent line}}$$
In this graph, drag the slider for $A+h$ towards $A$ to make $h$ smaller. Watch how the blue secant line (through two points) becomes the green tangent line (touching at one point) as $h \to 0$.
The Derivative Function
Instead of finding the derivative at ONE specific point, we can find a formula for the derivative at ANY point:
$$f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$$
This gives us a new function $f'(x)$ that outputs the slope at every x-value.
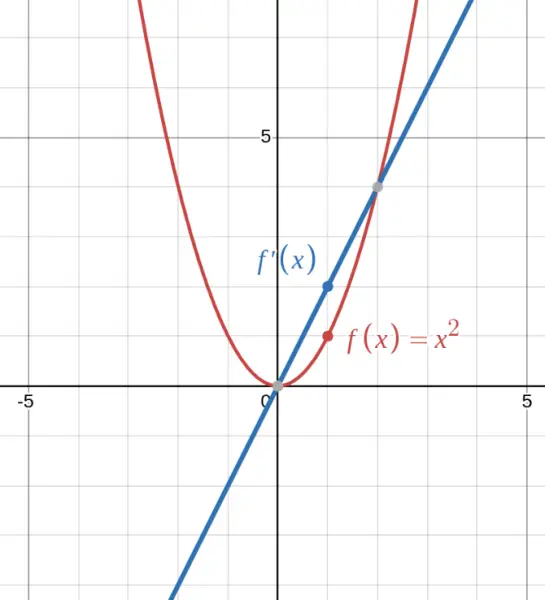
In this graph, notice that when $f(x) = x^2$ is decreasing (left of $x = 0$), its derivative $f'(x) = 2x$ is negative. When $f(x)$ is increasing (right of $x = 0$), the derivative is positive. At $x = 0$, the derivative is zero (horizontal tangent).
Notation
All of these mean "the derivative of $y$ with respect to $x$":
| Notation | Read as | When to use |
|---|---|---|
| $f'(x)$ | "f prime of x" | Most common |
| $\frac{dy}{dx}$ | "dee y dee x" | When $y = f(x)$ |
| $\frac{d}{dx}[f(x)]$ | "the derivative of f" | When applying rules |
| $Df(x)$ | "D of f" | Less common |
Problem: Find $f'(x)$ using the limit definition if $f(x) = x^2$.
Step 1: Write the limit definition
$$f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$$
Step 2: Calculate $f(x+h)$
$$f(x+h) = (x+h)^2 = x^2 + 2xh + h^2$$
Step 3: Substitute into the formula
$$f'(x) = \lim_{h \to 0} \frac{(x^2 + 2xh + h^2) - x^2}{h}$$
Step 4: Simplify the numerator
$$= \lim_{h \to 0} \frac{2xh + h^2}{h}$$
Step 5: Factor out $h$ and cancel
$$= \lim_{h \to 0} \frac{h(2x + h)}{h} = \lim_{h \to 0} (2x + h)$$
Step 6: Evaluate the limit
$$= 2x + 0 = \boxed{2x}$$
Problem: Find $f'(4)$ using the limit definition if $f(x) = \sqrt{x}$.
Note: This example uses Form 2 — the $x \to a$ definition. Compare to the other examples which use Form 1.
Step 1: Set up using the alternate form with $a = 4$
$$f'(4) = \lim_{x \to 4} \frac{f(x) - f(4)}{x - 4} = \lim_{x \to 4} \frac{\sqrt{x} - 2}{x - 4}$$
Step 2: Rationalize the numerator
$$= \lim_{x \to 4} \frac{\sqrt{x} - 2}{x - 4} \cdot \frac{\sqrt{x} + 2}{\sqrt{x} + 2} = \lim_{x \to 4} \frac{x - 4}{(x-4)(\sqrt{x} + 2)}$$
Step 3: Cancel $(x - 4)$
$$= \lim_{x \to 4} \frac{1}{\sqrt{x} + 2}$$
Step 4: Evaluate the limit
$$= \frac{1}{\sqrt{4} + 2} = \frac{1}{2 + 2} = \frac{1}{4}$$
$$\boxed{f'(4) = \frac{1}{4}}$$
Problem: Find $f'(3)$ using the limit definition if $f(x) = \frac{1}{x}$.
Step 1: Set up the formula with $a = 3$
$$f'(3) = \lim_{h \to 0} \frac{f(3+h) - f(3)}{h} = \lim_{h \to 0} \frac{\frac{1}{3+h} - \frac{1}{3}}{h}$$
Step 2: Combine fractions in the numerator
$$\frac{1}{3+h} - \frac{1}{3} = \frac{3 - (3+h)}{3(3+h)} = \frac{-h}{3(3+h)}$$
Step 3: Divide by $h$
$$f'(3) = \lim_{h \to 0} \frac{-h}{3(3+h)} \cdot \frac{1}{h} = \lim_{h \to 0} \frac{-1}{3(3+h)}$$
Step 4: Evaluate the limit
$$= \frac{-1}{3(3+0)} = \frac{-1}{9}$$
$$\boxed{f'(3) = -\frac{1}{9}}$$
Problem: Find $f'(x)$ using the limit definition if $f(x) = \sqrt{x}$.
Note: This example finds the derivative as a function (not at a single point), using Form 1.
Step 1: Set up the limit
$$f'(x) = \lim_{h \to 0} \frac{\sqrt{x+h} - \sqrt{x}}{h}$$
Step 2: Rationalize by multiplying by the conjugate
$$= \lim_{h \to 0} \frac{\sqrt{x+h} - \sqrt{x}}{h} \cdot \frac{\sqrt{x+h} + \sqrt{x}}{\sqrt{x+h} + \sqrt{x}}$$
Step 3: Simplify the numerator using $(a-b)(a+b) = a^2 - b^2$
$$= \lim_{h \to 0} \frac{(x+h) - x}{h(\sqrt{x+h} + \sqrt{x})} = \lim_{h \to 0} \frac{h}{h(\sqrt{x+h} + \sqrt{x})}$$
Step 4: Cancel $h$
$$= \lim_{h \to 0} \frac{1}{\sqrt{x+h} + \sqrt{x}}$$
Step 5: Evaluate the limit
$$= \frac{1}{\sqrt{x} + \sqrt{x}} = \frac{1}{2\sqrt{x}}$$
$$\boxed{f'(x) = \frac{1}{2\sqrt{x}}}$$
When Does the Derivative NOT Exist?
The derivative fails to exist at points where:
| Situation | What Happens | Example |
|---|---|---|
| Sharp corner | Left and right slopes are different | $f(x) = |x|$ at $x = 0$ |
| Vertical tangent | Slope is $\pm\infty$ | $f(x) = \sqrt[3]{x}$ at $x = 0$ |
| Discontinuity | Function jumps or has a hole | Any discontinuous function |
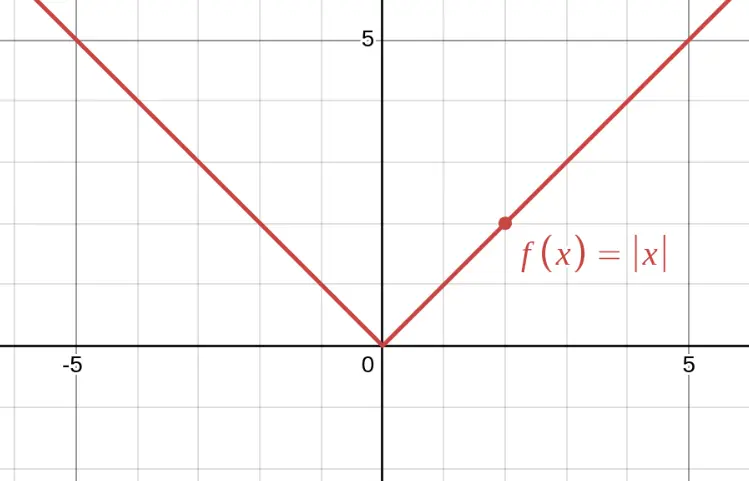
In this graph, $f(x) = |x|$ has a sharp corner at $x = 0$. The slope from the left is $-1$, and the slope from the right is $+1$. Since these don't match, $f'(0)$ does not exist.
Key Relationship: Differentiability and Continuity
$$\text{Differentiable at } a \implies \text{Continuous at } a$$
But the reverse is NOT true!
$$\text{Continuous at } a \not\Rightarrow \text{Differentiable at } a$$
Example: $f(x) = |x|$ is continuous at $x = 0$ (no break in the graph), but NOT differentiable at $x = 0$ (sharp corner).
Common Mistakes and Misunderstandings
❌ Mistake: Forgetting to expand $(x+h)^2$ correctly
Wrong: $(x+h)^2 = x^2 + h^2$
Why it's wrong: You're missing the middle term! Use FOIL or the formula $(a+b)^2 = a^2 + 2ab + b^2$.
Correct: $(x+h)^2 = x^2 + 2xh + h^2$
❌ Mistake: Plugging in $h = 0$ too early
Wrong: $\displaystyle\frac{f(x+0) - f(x)}{0} = \frac{0}{0}$... stuck!
Why it's wrong: You must simplify algebraically FIRST to cancel the $h$ in the denominator, THEN take the limit.
Correct: Simplify until you can cancel $h$, then let $h \to 0$.
❌ Mistake: Confusing the two forms of the definition
Wrong: Mixing up $\displaystyle\lim_{h \to 0} \frac{f(x) - f(a)}{h}$
Why it's wrong: The two forms are:
- $\displaystyle\lim_{h \to 0} \frac{f(a+h) - f(a)}{h}$ — uses $h$ as the small change
- $\displaystyle\lim_{x \to a} \frac{f(x) - f(a)}{x - a}$ — uses $x$ approaching $a$
Don't mix the variables!
Correct: Pick one form and stick with it consistently.
❌ Mistake: Thinking continuity guarantees differentiability
Wrong: "The function is continuous, so it must be differentiable."
Why it's wrong: Continuity is necessary but NOT sufficient. Sharp corners (like $|x|$) and vertical tangents (like $\sqrt[3]{x}$) are continuous but not differentiable.
Correct: Differentiable $\Rightarrow$ Continuous, but Continuous $\not\Rightarrow$ Differentiable.
❌ Mistake: Forgetting to rationalize for square roots
Wrong: Getting stuck on $\displaystyle\lim_{h \to 0} \frac{\sqrt{x+h} - \sqrt{x}}{h}$
Why it's wrong: Direct substitution gives $\frac{0}{0}$. You need to multiply by the conjugate to simplify.
Correct: Multiply top and bottom by $(\sqrt{x+h} + \sqrt{x})$ to rationalize the numerator.
Definition of the Derivative (Limit Form)
The derivative of f at x is defined as this limit, representing the instantaneous rate of change
Variables:
- $f'(x)$:
- the derivative of f at x
- $h$:
- a small change in x (approaches 0)
- $f(x+h)$:
- function value at x+h
- $f(x)$:
- function value at x
Definition of the Derivative (Alternate Form)
Equivalent definition using x approaching a instead of h approaching 0
Variables:
- $f'(a)$:
- the derivative of f at the point a
- $a$:
- the point where we evaluate the derivative
- $x$:
- variable approaching a
- $f(x) - f(a)$:
- change in function value
- $x - a$:
- change in input
Difference Quotient
The slope of the secant line between (x, f(x)) and (x+h, f(x+h)). The derivative is the limit of this as h approaches 0
Variables:
- $f(x+h) - f(x)$:
- rise (change in y)
- $h$:
- run (change in x)
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.