Domain and Range for MATH 139
Exam Relevance for MATH 139
Often tested as part of function analysis. Know domain restrictions from denominators, square roots, and logarithms.
What is Domain and Range?
Every function is like a machine: you put something in (the input), and you get something out (the output). But not every machine accepts every input — and not every output is possible.
- Domain = all the valid inputs (x-values) you can plug into the function
- Range = all the possible outputs (y-values) the function can produce
Understanding domain and range helps you know where a function "lives" — which values make sense to use and which results you can expect.
Visualizing Domain and Range
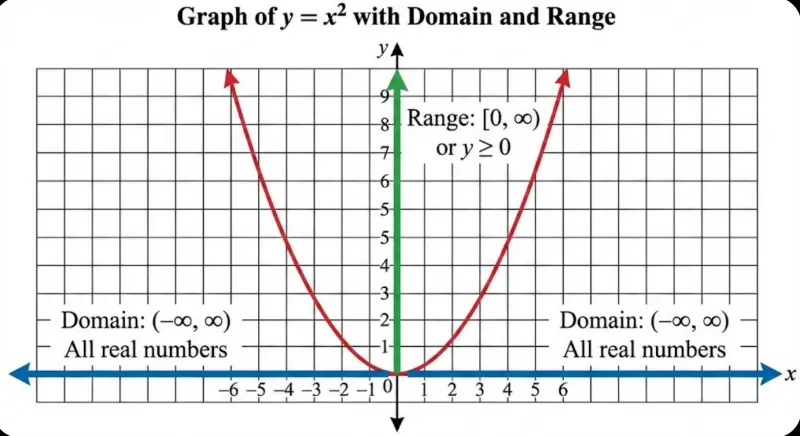
In this graph, notice that:
- Domain: You can plug in ANY x-value (the parabola extends left and right forever) → Domain: $(-\infty, \infty)$
- Range: The outputs only go from 0 upward (the parabola never dips below the x-axis) → Range: $[0, \infty)$
Interval Notation Quick Reference
| Notation | Meaning | When to Use |
|---|---|---|
| $(a, b)$ | All numbers between $a$ and $b$, not including $a$ or $b$ | Open interval |
| $[a, b]$ | All numbers between $a$ and $b$, including $a$ and $b$ | Closed interval |
| $[a, b)$ | Includes $a$, excludes $b$ | Half-open |
| $(-\infty, a)$ | All numbers less than $a$ | Unbounded left |
| $(a, \infty)$ | All numbers greater than $a$ | Unbounded right |
| $(-\infty, \infty)$ | All real numbers | No restrictions |
💡 Key rule: Always use parentheses with $\infty$ or $-\infty$ — you can never "reach" infinity, so you can't include it!
Finding the Domain
The domain is usually "all real numbers" except where the function breaks. Look for these common restrictions:
Restriction 1: Division by Zero
You cannot divide by zero. If the function has a denominator, set it $\neq 0$.
$$f(x) = \frac{1}{x-3}$$
The denominator is $x - 3$. Set it $\neq 0$:
$$x - 3 \neq 0 \implies x \neq 3$$
Domain: $(-\infty, 3) \cup (3, \infty)$ — all real numbers except 3.
Restriction 2: Square Roots of Negatives
You cannot take the square root of a negative number (in real numbers). The expression under the root must be $\geq 0$.
$$g(x) = \sqrt{x + 2}$$
Set the inside $\geq 0$:
$$x + 2 \geq 0 \implies x \geq -2$$
Domain: $[-2, \infty)$
Restriction 3: Logarithms of Non-Positives
You cannot take the logarithm of zero or a negative number. The input to a log must be $> 0$.
$$h(x) = \ln(x - 5)$$
Set the inside $> 0$:
$$x - 5 > 0 \implies x > 5$$
Domain: $(5, \infty)$
Combining Restrictions
Some functions have multiple restrictions. Find each one, then combine.
$$f(x) = \frac{\sqrt{x}}{x - 4}$$
- Square root: $x \geq 0$
- Denominator: $x \neq 4$
Domain: $[0, 4) \cup (4, \infty)$
Finding the Range
The range is often trickier than the domain. Here are strategies:
Strategy 1: Use the Graph
For $f(x) = \frac{1}{x}$:
- The graph approaches but never touches $y = 0$
- The function produces every other y-value
- Range: $(-\infty, 0) \cup (0, \infty)$ — all real numbers except 0
Strategy 2: Think About What Outputs Are Possible
For $f(x) = x^2$:
- Squaring any number gives a non-negative result
- You can get 0 (when $x = 0$)
- You can get arbitrarily large values (as $x \to \pm\infty$)
- Range: $[0, \infty)$
Strategy 3: Solve for x in Terms of y
Set $y = f(x)$ and solve for $x$. The values of $y$ that give valid solutions are in the range.
For $f(x) = 2x + 1$:
$$y = 2x + 1$$ $$y - 1 = 2x$$ $$x = \frac{y - 1}{2}$$
This gives a valid $x$ for ANY value of $y$. Range: $(-\infty, \infty)$
Find the domain and range of $f(x) = \sqrt{9 - x^2}$.
Step 1: Find the domain
The expression under the square root must be $\geq 0$:
$$9 - x^2 \geq 0$$ $$9 \geq x^2$$ $$-3 \leq x \leq 3$$
Domain: $[-3, 3]$
Step 2: Find the range
- The minimum value of $\sqrt{9 - x^2}$ is $0$ (when $x = \pm 3$)
- The maximum value is $\sqrt{9} = 3$ (when $x = 0$)
Range: $[0, 3]$
Step 3: Visualize
This is actually the top half of a circle with radius 3!
Find the domain and range of $f(x) = \frac{x + 1}{x - 2}$.
Step 1: Find the domain
Denominator $\neq 0$:
$$x - 2 \neq 0 \implies x \neq 2$$
Domain: $(-\infty, 2) \cup (2, \infty)$
Step 2: Find the range
Solve for $x$:
$$y = \frac{x + 1}{x - 2}$$
$$y(x - 2) = x + 1$$
$$yx - 2y = x + 1$$
$$yx - x = 2y + 1$$
$$x(y - 1) = 2y + 1$$
$$x = \frac{2y + 1}{y - 1}$$
This is undefined when $y = 1$. So $y = 1$ is NOT in the range.
Range: $(-\infty, 1) \cup (1, \infty)$
Using the graph below, find the domain and range of the piecewise function.
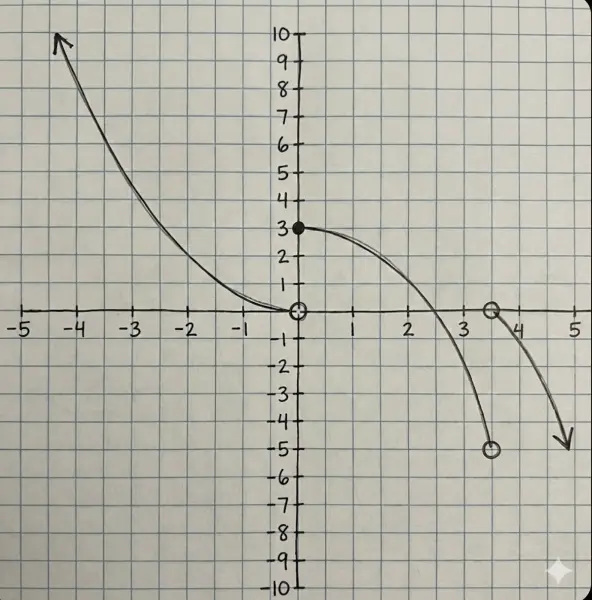
When reading domain and range from a graph:
- Domain: Look at how far left and right the graph extends (x-axis coverage)
- Range: Look at how far up and down the graph extends (y-axis coverage)
- Closed dots (●) mean the point IS included — use a bracket $[$
- Open dots (○) mean the point is NOT included — use a parenthesis $($
Finding the Domain:
- The first piece extends from the upper left (toward $x = -\infty$) and ends at $x = 0$ with an open circle
- The second piece starts at $x = 0$ with a closed dot and ends at $x = 3.5$ with an open circle
- The third piece starts at $x = 3.5$ with an open circle and extends to the lower right (toward $x = +\infty$)
At $x = 0$: The closed dot means $x = 0$ IS included.
At $x = 3.5$: Both adjacent pieces have open circles, so $x = 3.5$ is NOT included.
$$\boxed{\text{Domain: } (-\infty, 3.5) \cup (3.5, \infty)}$$
Finding the Range:
- The first piece has an arrow pointing up toward $+\infty$
- The third piece has an arrow pointing down toward $-\infty$
- Together, every y-value from $-\infty$ to $+\infty$ is covered
$$\boxed{\text{Range: } (-\infty, \infty)}$$
Common Mistakes and Misunderstandings
❌ Mistake: Using brackets with infinity
Wrong: $[0, \infty]$
Why it's wrong: Infinity is not a number — you can never "reach" it. You can't include something that doesn't exist as a specific value.
Correct: $[0, \infty)$
❌ Mistake: Forgetting to check ALL restrictions
Wrong: For $f(x) = \frac{\sqrt{x}}{x-1}$, saying domain is $x \neq 1$
Why it's wrong: You found the denominator restriction but forgot the square root restriction ($x \geq 0$).
Correct: Domain: $[0, 1) \cup (1, \infty)$
❌ Mistake: Confusing domain and range
Wrong: "The range of $f(x) = x^2$ is all real numbers because you can plug in any x."
Why it's wrong: That describes the domain, not the range. The range asks what outputs are possible.
Correct: Domain: $(-\infty, \infty)$. Range: $[0, \infty)$ because $x^2$ is never negative.
Domain
The set of all valid input values (x-values) for which the function produces a real output.
Variables:
- $x$:
- input value
- $f(x)$:
- the function
Range
The set of all possible output values (y-values) that the function can produce.
Variables:
- $y$:
- output value
- $f(x)$:
- the function
- $x$:
- input from the domain
Square Root Domain Restriction
For real numbers, you cannot take the square root of a negative. Set the expression under the root ≥ 0 and solve.
Variables:
- $\text{expression}$:
- whatever is under the square root
Denominator Restriction
Division by zero is undefined. Set the denominator ≠ 0 and solve to find excluded values.
Variables:
- $\text{denominator}$:
- the bottom of the fraction
Logarithm Domain Restriction
Logarithms are only defined for positive inputs. Set the expression inside the log > 0 and solve.
Variables:
- $\text{expression}$:
- the input to the logarithm
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.