Practice Final #2
Full CourseExam Settings
Mixed Content
Mixed Content(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
We are trying to evaluate:
We can rewrite this as:
By splitting it like this, we can analyze each part separately, making it easier to solve.
1. **Evaluate** :
This is a standard limit that often appears in exams.
[Remember this limit:
They love to test this! It shows that and are almost identical for small values of .]
2. **Evaluate** :
For small , the function behaves similarly to .
[This limit is another must-know:
This shows that for small , the numerator and denominator act like the same function.]
3. **Evaluate** :
This tells us that the function grows without bound as approaches 0 from the positive side.
Using the property that:
**(only if all limits are finite or one limit goes to infinity without any undefined behavior like )**, we get:
Since the multiplication involves finite values and one , the result is:
This approach works here because each limit we evaluated behaves predictably and does not lead to an undefined form like . Therefore, we can confidently multiply the individual limits.
In this tough question they are testing your knowledge of the these two limits:
and
. As long as you know those limits then you'll have no problem with this question.
The reciprocal of each limit is also 1:
These limits show that and behave almost exactly like when is close to 0. Knowing these will help you solve many tricky limits that appear in calculus exams!
You can also therefore mix these terms:
Both and behave like when is close to 0, so this limit simplifies to:
This is another handy limit to keep in mind for calculus exams!
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
We can multiply and divide the expression by its conjugate:
This simplifies to:
So the expression becomes:
As , the term behaves similarly to because dominates inside the square root. Thus:
So the denominator becomes approximately:
Now, the expression becomes:
Thus, the correct answer is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
We recognize that the integral of is the well-known inverse tangent function:
The integral of is:
Now we combine the two integrals:
where is the most general constant of integration.
Thus, the most general antiderivative is:
The correct answer is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
What is the rate of change when ?
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
Using the product rule on the left side:
The derivative of the right side is:
Now apply the product rule to the left side:
This simplifies to:
First, isolate the term with :
Now, divide both sides by to get:
When , the expression becomes:
Thus, the rate of change when is:
The correct answer is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
The distance from any point on the parabola to the origin is:
We want to minimize this distance. Since minimizing the square of the distance is easier, we’ll minimize:
Take the derivative of and set it to 0:
Set the derivative equal to 0:
Factor out :
Solutions:
For :
For :
The -coordinates closest to the origin are:
Thus, the correct answer is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
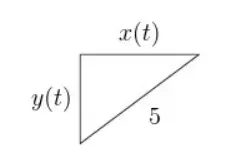
Figure: right triangle
What is the ratio when ? Assume that is non-zero.
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
We are given a right-angled triangle with a hypotenuse that is always 5 cm long. The sides are , , and the hypotenuse is . So the Pythagorean theorem gives:
Simplify:
Divide both sides by :
Thus:
Using the Pythagorean theorem:
The ratio when is:
Thus, the correct answer is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
We use logarithmic differentiation. Take the natural logarithm of both sides:
Using the chain rule on the left side, the derivative of is:
This term comes from the **chain rule**. When differentiating , we first take and then multiply by the derivative of the inner function , which gives:
On the right side, we apply the **product rule**:
We need to find . Start by plugging in into the right side:
Since:
This simplifies to:
Now, multiply both sides by . At , we have:
Thus:
The value of is:
Thus, the correct answer is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
at the point .
What is ? (2.5 points)
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
We use the quotient rule to differentiate:
The quotient rule states:
where and .
Now:
Simplify:
Thus:
The slope of the tangent line at is:
Thus, the correct answer is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
at the point .
What is ? (2.5 points)
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
We already know the derivative is:
Evaluating it at :
So:
Thus, the point is:
The equation of the line is:
Substitute and :
Simplify:
Solve for :
The -intercept is:
Thus, the correct answer is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
Since higher-order terms become negligibly small for small , we approximate:
Factor out :
**Remember:** The approximation is useful for small .
Using this approximation:
Simplify:
The value of the limit is:
Thus, the correct answer is:
This question is trying to teach you something about the comparative size of these two functions as we get closer to 0.
It turns out that is about bigger than as we get close to 0, even though they both approach . That's what this question is trying to teach you!
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
A function is continuous at if:
Using Taylor expansions:
Thus:
The smallest positive value is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
*Note:* The vertex of a parabola is the point .
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
The parabola is given by the equation:
The roots are and , and the **distance between the roots** is:
The vertex of the parabola lies at the midpoint of the roots. The x-coordinate of the vertex is:
The **y-coordinate of the vertex** is given by:
Since the equation has a negative coefficient for the quadratic term, the parabola opens downward, meaning the vertex represents a maximum point.
To find how the -coordinate of the vertex changes with time, we differentiate the formula for with respect to time :
Simplify the expression:
Given that:
substitute these values into the equation:
Thus, the rate of change of the -coordinate of the vertex is:
The negative sign means the vertex is moving downward as the roots move apart.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
*Don't forget to show that your answer is a minimum and not a maximum!*
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
The volume is:
The surface area is:
Solve for :
Substitute into the surface area formula:
Take the derivative:
Set the derivative equal to 0:
Thus:
Since , we substitute:
To confirm that this is a minimum, we take the second derivative:
Since , both terms are positive:
This confirms the solution corresponds to a minimum.
The dimensions that minimize the material used are:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Sub-questions:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
The function is:
Both (a polynomial) and (an exponential function) are continuous for all . Therefore, the sum of these functions is continuous everywhere.
**Step 1: Find the First Derivative **
Using the product rule:
Applying the product rule to the first term:
Simplify:
Factor out :
**Step 2: Solve for Critical Points**
Since for all real , solve:
**Critical Points:**
**Step 1: Find the Second Derivative **
Using the product rule on the first derivative:
Differentiate:
The derivative of is:
Now substitute:
Simplify:
Factor out :
**Step 2: Solve for Inflection Points**
Since , solve:
This gives two cases:
1. .
2. .
Solve the second equation:
**Inflection Points:**
---
- **Discontinuities:** None.
- **Critical Points:** .
- **Inflection Points:**
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
- **Critical Points:** .
- **Inflection Points:**
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
We are analyzing the function:
Horizontal asymptotes occur when the function approaches a constant value as or .
Since very quickly as , the first term also approaches 0:
Now, check the behavior as :
Similarly, as , the term also approaches 0:
**Horizontal Asymptote:**
---
A **vertical asymptote** occurs when the function becomes arbitrarily large (positively or negatively) as approaches a specific finite value. More formally, a function has a vertical asymptote at if:
Such asymptotic behavior typically arises when:
- The function has a division by zero, such as in .
- There are logarithmic terms, like , which decrease without bound as the input approaches a critical point.
- Or other forms of singularities that force the function to grow indefinitely large.
---
### Step 2.1: Analyze the Function
We now analyze the structure of the given function. It contains:
- A linear term .
- An exponential decay term , which approaches rapidly as or .
We are checking if there are any values of for which the function becomes undefined or grows without bound.
---
### Step 2.2: Look for Potential Asymptotes
Let’s examine the key term :
1. **Behavior as :**
- As increases, decays very quickly to . This decay outpaces the growth of the linear term .
- Therefore, the product as .
2. **Behavior as :**
- Similarly, as becomes increasingly negative, the term also approaches , and the product again approaches .
Because the function remains finite in both directions and there are no divisions by zero or undefined values for any finite , the function is continuous across all real numbers.
---
**Conclusion: There are no vertical asymptotes.** The function is well-defined and continuous everywhere for , with no points where the function becomes arbitrarily large or undefined.
- **Horizontal Asymptote:** .
- **Vertical Asymptotes:** None.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
- **Vertical Asymptotes:** None.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Figure 1: all critical points, inflection points, and asymptotes
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Figure 1: all critical points, inflection points, and asymptotes
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Sub-questions:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
To find the explicit formula for , we integrate twice.
where is a constant of integration.
where is another constant of integration.
Given:
- ,
- .
Apply the first initial condition :
Apply the second initial condition :
Substitute :
(a) The explicit formula for is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
(b) The time when is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Alice wins the race! Use the Mean Value Theorem to rigorously prove that there is a time when the velocity of Alice was strictly greater than the velocity of Bob.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
Define the function:
where and are the positions of Alice and Bob at time , respectively. This function represents the difference in their positions.
Since is continuous on and differentiable on , the Mean Value Theorem guarantees that there exists a point such that:
Since Alice wins the race, her final position is greater than Bob’s, meaning:
Both runners start from the same point, so:
Thus, the expression for becomes:
Since:
it follows that:
Using the Mean Value Theorem on the difference function , we have rigorously shown that there exists a time when Alice’s velocity was strictly greater than Bob’s:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Let:
where and are the positions of Alice and Bob, respectively.
Since is continuous and differentiable, the Mean Value Theorem guarantees a point such that:
Since Alice wins, , so:
Thus:
Since:
we conclude: