Practice Final #2
Full CourseExam Settings
Short Answer Questions
Short AnswerExercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
First, notice that as , the expression inside the parentheses approaches 1, while the exponent approaches . This gives the indeterminate form , which often suggests that the limit involves the exponential function, . Our goal is to manipulate the expression to fit the standard form for the definition of . We can do this by rewriting the base, , into the form .
By rewriting as , we can split the fraction. This isolates a '1' which is crucial for the next step.
The key formula to remember is the limit definition of the exponential function: . Our entire strategy is to make our limit look like this form.
Now that our limit looks very similar to the definition, we can use a substitution to make it match perfectly.
Let . As , it's also true that . From this substitution, we also have . After substituting, we can split the exponent using the property . This allows us to separate the expression into two parts. The first part will match the definition of exactly, and the second part will be a simple limit to evaluate.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We need to find by taking the derivative of each term:
Now we take the derivative of to find :
When taking derivatives of trigonometric functions with coefficients in the argument, remember the chain rule: and .
Now we substitute into our expression for :
We know that:
-
-
Therefore:
Therefore:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We already found that:
Setting the derivative equal to zero:
Since the denominator is never zero on our interval, we have:
This gives us or . Since is outside our interval , we only consider .
We need to check the function value at , , and .
At :
At :
At :
Comparing all three values:
-
-
-
The maximum value is which occurs at .
For rational functions, the behavior may be very different on different intervals. Always check all critical points within the interval AND both endpoints!
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We already found the derivative of this function in our previous question:
To find critical points, we set this equal to zero:
Since the denominator cannot be zero on our interval (as when ), we only need:
So or are our critical points.
Our interval is , and we found one critical point at which is within this interval.
Extreme Value Theorem tells us that the maximum must occur either at a critical point within the interval or at an endpoint.
We need to evaluate the function at , , and .
When finding extreme values on a closed interval, always check both the critical points inside the interval AND the endpoint values!
Comparing all three values:
-
-
-
The maximum value is which occurs at .
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Since we have a fraction, we'll use the quotient rule.
If , then:
Let's set:
-
-
When evaluating at x = 0, remember that and , which simplifies our work considerably!
At :
Therefore:
Mcq Questions
MCQat the point .
What is ? (2.5 points)
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
We already know the derivative is:
Evaluating it at :
So:
Thus, the point is:
The equation of the line is:
Substitute and :
Simplify:
Solve for :
The -intercept is:
Thus, the correct answer is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
at the point .
What is ? (2.5 points)
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
We use the quotient rule to differentiate:
The quotient rule states:
where and .
Now:
Simplify:
Thus:
The slope of the tangent line at is:
Thus, the correct answer is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
We use logarithmic differentiation. Take the natural logarithm of both sides:
Using the chain rule on the left side, the derivative of is:
This term comes from the **chain rule**. When differentiating , we first take and then multiply by the derivative of the inner function , which gives:
On the right side, we apply the **product rule**:
We need to find . Start by plugging in into the right side:
Since:
This simplifies to:
Now, multiply both sides by . At , we have:
Thus:
The value of is:
Thus, the correct answer is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
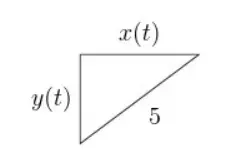
Figure: right triangle
What is the ratio when ? Assume that is non-zero.
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
We are given a right-angled triangle with a hypotenuse that is always 5 cm long. The sides are , , and the hypotenuse is . So the Pythagorean theorem gives:
Simplify:
Divide both sides by :
Thus:
Using the Pythagorean theorem:
The ratio when is:
Thus, the correct answer is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
(A)
(B)
(C)
(D)
(E)
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
The distance from any point on the parabola to the origin is:
We want to minimize this distance. Since minimizing the square of the distance is easier, we’ll minimize:
Take the derivative of and set it to 0:
Set the derivative equal to 0:
Factor out :
Solutions:
For :
For :
The -coordinates closest to the origin are:
Thus, the correct answer is:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Long Answer Questions
Long AnswerExercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Let's check what happens when we try to evaluate the limit directly:
As :
-
-
So we have the indeterminate form , which we can't evaluate directly.
To handle this indeterminate form, I'll define:
Taking the natural logarithm of both sides:
Using the property of logarithms:
Now we need to evaluate:
As :
-
-
So we have the indeterminate form , which means we can apply L'Hôpital's Rule.
Finding the derivatives:
Applying L'Hôpital's Rule:
For this new limit:
As :
-
-
We again have the indeterminate form , so we apply L'Hôpital's Rule again.
Finding the derivatives:
Applying L'Hôpital's Rule:
As :
-
So:
We found that , so:
For indeterminate forms like , always try the strategy of taking the natural logarithm first, then applying L'Hôpital's Rule to the resulting expression.
Therefore:
Determine where the function is increasing and decreasing.
Determine where the function is concave up and concave down.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Let's work with the function:
To find the first derivative, I'll use the product rule:
Where:
-
-
First, I'll find :
Now applying the product rule:
For the second derivative, I'll apply the product rule again to
Where:
-
-
First, I'll find :
Now applying the product rule:
A function is increasing when and decreasing when .
Let's find where :
Since for all , we need to solve:
This gives us or
When analyzing where a function is increasing or decreasing, focus on where the first derivative changes sign.
Testing regions:
- For : and , so , meaning
- For : and , so , meaning
- For : and , so , meaning
Therefore:
- is increasing for
- is decreasing for
- is increasing for
A function is concave up when and concave down when .
From our second derivative:
Since for all , we need to solve :
Testing regions:
- For : , so
- For : , so
- For : , so
Therefore:
- is concave up for
- is concave down for
- is concave up for
Classify each such point as a local minimum, a local maximum or some other kind of critical point.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Let's work with the function: in the interval .
To find critical points, I need to take the derivative and set it equal to zero.
When differentiating products, remember that the derivative of follows the product rule:
This equation equals zero when either:
- , which gives
- , which gives where is an integer
In our interval , when:
So our critical points are:
-
-
-
-
To classify, I'll use the second derivative test.
Now I'll evaluate at each critical point:
At :
Since , this is a local minimum.
At :
Since , this is a local maximum.
At :
Since , this is a local minimum.
At :
Since , this is a local maximum.
Figure: solution
Word Problem Questions
Word ProblemWhen reaching and , the rate of change in the -direction is given by . What is at this point?
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
To find , we need to implicitly differentiate the equation with respect to , applying the chain rule to each term.
Starting with:
Differentiate each term with respect to :
**First term**:
**Second term**:
**Third term**:
Using the product rule:
Now, combine all terms:
Group the terms:
Substitute , , and :
Simplify each term:
Solve for :
Alice wins the race! Use the Mean Value Theorem to rigorously prove that there is a time when the velocity of Alice was strictly greater than the velocity of Bob.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
Define the function:
where and are the positions of Alice and Bob at time , respectively. This function represents the difference in their positions.
Since is continuous on and differentiable on , the Mean Value Theorem guarantees that there exists a point such that:
Since Alice wins the race, her final position is greater than Bob’s, meaning:
Both runners start from the same point, so:
Thus, the expression for becomes:
Since:
it follows that:
Using the Mean Value Theorem on the difference function , we have rigorously shown that there exists a time when Alice’s velocity was strictly greater than Bob’s:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Let:
where and are the positions of Alice and Bob, respectively.
Since is continuous and differentiable, the Mean Value Theorem guarantees a point such that:
Since Alice wins, , so:
Thus:
Since:
we conclude:
Multi Part Questions
Multi-PartExercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Sub-questions:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
To show that has at least one zero in , we can apply the **Intermediate Value Theorem**, which states:
Intermediate Value Theorem: If is continuous on and and have opposite signs, then there exists at least one such that .
The function is a polynomial, and polynomials are continuous everywhere. Therefore, is continuous on .
Evaluate :
Evaluate :
Since and , and have opposite signs. By the Intermediate Value Theorem, there must be at least one such that .
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
To show that has only one zero in , we can examine the behavior of the function by analyzing its derivative . If does not change sign in , then is either strictly increasing or strictly decreasing on that interval, implying at most one zero.
Given:
Differentiate to find :
Since , note that each term and is non-negative for . Therefore, for all , and only at .
Since on , is non-decreasing on this interval. This implies that can have at most one zero in , as a non-decreasing function cannot cross the x-axis more than once without changing direction.
Since is continuous on and has a zero in this interval (from part (a)), and since is non-decreasing on , we conclude that the zero is unique.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Sub-questions:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
To find the maximum, we need to calculate the derivative and set it to zero to find critical points. We’ll use the product rule since is the product of and .
**Using the product rule**:
Let:
-
-
Then:
-
-
So,
Combine terms:
Simplify the expression inside the parentheses:
Now, set :
Since , we only need to solve:
Factoring gives:
So, and . However, since we are only interested in the interval , we discard and keep .
Now, evaluate at , , and :
**At** :
**At** :
**At** :
Now, compare the values at , , and :
Since and , the maximum value occurs at with .
This question is designed to test your understanding of the product rule, as well as evaluating functions at critical points and endpoints to find absolute maximums or minimums. The professor likely included this question to ensure you can handle more complex functions and apply calculus principles over a specified interval.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
To determine where is concave down, we need to find the second derivative and determine where it is negative.
Recall that . We already found the first derivative:
Now, we’ll differentiate again to find , using the product rule.
Let:
-
-
Then:
-
-
Applying the product rule:
Substitute , , , and :
Combine terms:
Simplify inside the parentheses:
To find where is concave down, we need .
Since for all , the sign of depends only on :
Solve this inequality by finding the roots of using the quadratic formula:
Now, we test the sign of in the intervals around these roots, namely, in the intervals , , and .
** Interval 1:
Choose a test point in this interval.
Substitute into :
Since , the function is positive in this interval.
**Interval 2:
Choose a test point in this interval.
Substitute into :
Since , the function is negative in this interval.
** Interval 3:
Choose a test point in this interval.
Substitute into :
Since , the function is positive in this interval.
Since the function is negative in the interval , this is the interval where the function is concave down.
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Unlock Premium Content
Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.
To find horizontal asymptotes, we examine the behavior of as approaches positive and negative infinity.
**As :**
The exponential term grows extremely fast as . Therefore, will also grow without bound because of , making .
**Conclusion**: There is no horizontal asymptote as .
**As :**
When , approaches because exponential functions decay towards zero for large negative inputs. Thus:
Since approaches as , there is a horizontal asymptote at:
Unlock Premium Content
Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.