Practice Final #4
Full CourseExam Settings
Mixed Content
Mixed ContentExercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
For the numerator:
For the denominator:
Therefore:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Evaluate the following limit:
Therefore:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
As :
- since grows much faster than
- for the same reason
When dealing with limits involving exponentials and trigonometric functions, remember that exponential functions like grow much faster than any polynomial or trigonometric function. Since sine and cosine are always bounded between -1 and 1, the ratio or will always approach 0 as approaches infinity.
Therefore:
(a) , (b) , (c) , (d) two asymptotes, (e) three asymptotes.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
(a) , (b) , (c) , (d) two asymptotes, (e) three asymptotes.
Vertical asymptotes occur at values where the denominator equals zero.
This gives us , , or as potential vertical asymptotes.
For these points to be vertical asymptotes, we need to verify that the numerator is non-zero at these points.
The numerator is . Since is always non-negative (as it's raised to an even power) and we're adding the positive constant 7, the expression under the square root is always positive. Therefore, the numerator is always positive and never zero.
Since the numerator is never zero at any of these points, all three values , , and are vertical asymptotes.
Since we've confirmed that the function has vertical asymptotes at , , and , there are three vertical asymptotes in total.
Therefore:
When analyzing rational functions with radicals, remember that expressions like (where k > 0) are always positive, ensuring that vertical asymptotes occur at all zeros of the denominator.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We need to use the power rule for differentiation:
For the first term:
For the second term:
Now we combine these results to find :
When we substitute :
Therefore:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We need to differentiate both sides of the equation with respect to :
Differentiating the left side:
Differentiating the right side:
At the point , we have and .
Let's substitute these values:
Now we need to calculate these values:
And:
Therefore:
We can simplify further:
Therefore:
When differentiating hyperbolic functions, remember that , similar to how the derivative of is for trigonometric functions.
Find the value of that makes continuous everywhere.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
For a piecewise function to be continuous at the transition point (in this case ), the limits from both sides must be equal:
The left-hand limit uses the first piece of the function:
The right-hand limit uses the second piece:
For continuity, these limits must be equal:
When working with piecewise functions, always check the value of each piece at the transition point to ensure continuity.
Therefore, the value of that makes continuous everywhere is:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We have a function with two terms:
1.
2.
We'll need to find the derivative of each term using the product rule, then evaluate at .
For the first term, , we use the product rule:
For the second term, , we use the product rule again:
When differentiating terms with , remember that . The coefficient comes out front!
The complete derivative is:
Now we evaluate at :
Therefore:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Since we have a fraction, we'll use the quotient rule.
If , then:
Let's set:
-
-
When evaluating at x = 0, remember that and , which simplifies our work considerably!
At :
Therefore:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Let and
Finding the derivatives:
Substituting into the quotient rule:
At :
The slope of the tangent line at is
Using the point-slope form of a line:
Let's find a point with a simple x-value, say :
Therefore, the point lies on the tangent line.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We already found the derivative of this function in our previous question:
To find critical points, we set this equal to zero:
Since the denominator cannot be zero on our interval (as when ), we only need:
So or are our critical points.
Our interval is , and we found one critical point at which is within this interval.
Extreme Value Theorem tells us that the maximum must occur either at a critical point within the interval or at an endpoint.
We need to evaluate the function at , , and .
When finding extreme values on a closed interval, always check both the critical points inside the interval AND the endpoint values!
Comparing all three values:
-
-
-
The maximum value is which occurs at .
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We already found that:
Setting the derivative equal to zero:
Since the denominator is never zero on our interval, we have:
This gives us or . Since is outside our interval , we only consider .
We need to check the function value at , , and .
At :
At :
At :
Comparing all three values:
-
-
-
The maximum value is which occurs at .
For rational functions, the behavior may be very different on different intervals. Always check all critical points within the interval AND both endpoints!
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We need to find by taking the derivative of each term:
Now we take the derivative of to find :
When taking derivatives of trigonometric functions with coefficients in the argument, remember the chain rule: and .
Now we substitute into our expression for :
We know that:
-
-
Therefore:
Therefore:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Let . Find the set on which the function is increasing.
When , , so:
When , , so:
Critical points occur when or when is undefined.
For :
This occurs when:
- , which is impossible for
- , which gives
For :
This occurs when:
- , which is impossible for
- , which gives , but this is outside our domain of
For :
Both formulations of the derivative approach 0 as approaches 0, so is also a critical point.
Therefore, our critical points are and .
For :
Since for , and for (because and ), we have for all .
For :
Since for , and for , we have for .
For :
Since for , and for , we have for .
Based on our analysis:
- For : (function is decreasing)
- For : (function is increasing)
- For : (function is decreasing)
- At and : (function is neither increasing nor decreasing)
Since we're looking for where the function is strictly increasing (not just non-decreasing), we exclude the critical points.
Therefore, the set on which is increasing is:
When finding intervals of increase/decrease, exclude critical points where the derivative equals zero, as the function is not strictly increasing or decreasing at those points.
(a) 7, (b) 11, (c) 14, (d) 16, (e) -80.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
The Intermediate Value Theorem states that if a function is continuous on a closed interval , then it takes on every value between and .
For the IVT to guarantee the existence of an where , the value must lie between and .
By the Intermediate Value Theorem, takes on all values between and for some in the interval .
Let's check each option:
- (a) 7: This is between and ✓
- (b) 11: This is NOT between and ✗
- (c) 14: This is NOT between and ✗
- (d) 16: This is NOT between and ✗
- (e) -80: This is NOT between and ✗
Only the value 7 lies between and , so it is the only value guaranteed by the Intermediate Value Theorem to be a value of for some in .
(a) 17, (b) 20, (c) 27, (d) 35, (e) -2.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
(a) 17, (b) 20, (c) 27, (d) 35, (e) -2.
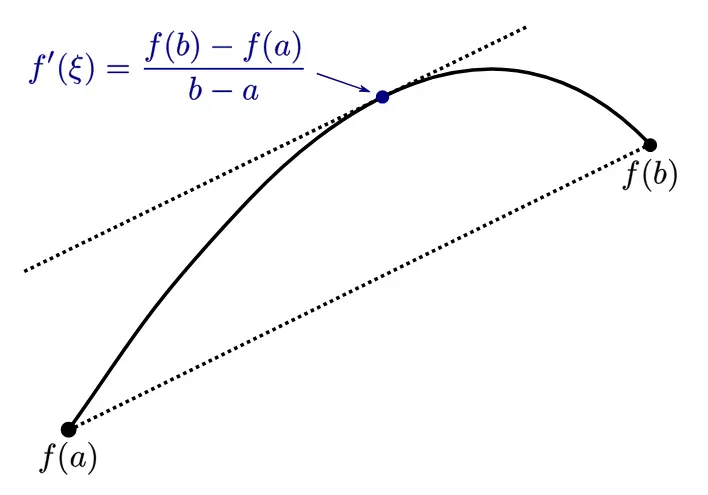
Figure: mean value theorem sample
This is just a sample. In our question we are using and instead of we use .
The Mean Value Theorem states that if a function is continuous on a closed interval and differentiable on the open interval , then there exists at least one point in such that:
The derivative at the special point equals the average rate of change of the function over the entire interval.
From our previous work, we already know:
By the Mean Value Theorem, there exists at least one point in the interval such that .
Looking at the answer choices:
- (a) 17: This matches our calculated value ✓
- (b) 20: Not equal to 17 ✗
- (c) 27: Not equal to 17 ✗
- (d) 35: Not equal to 17 ✗
- (e) -2: Not equal to 17 ✗
Classify each such point as a local minimum, a local maximum or some other kind of critical point.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Let's work with the function: in the interval .
To find critical points, I need to take the derivative and set it equal to zero.
When differentiating products, remember that the derivative of follows the product rule:
This equation equals zero when either:
- , which gives
- , which gives where is an integer
In our interval , when:
So our critical points are:
-
-
-
-
To classify, I'll use the second derivative test.
Now I'll evaluate at each critical point:
At :
Since , this is a local minimum.
At :
Since , this is a local maximum.
At :
Since , this is a local minimum.
At :
Since , this is a local maximum.
Figure: solution
Determine where the function is increasing and decreasing.
Determine where the function is concave up and concave down.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Let's work with the function:
To find the first derivative, I'll use the product rule:
Where:
-
-
First, I'll find :
Now applying the product rule:
For the second derivative, I'll apply the product rule again to
Where:
-
-
First, I'll find :
Now applying the product rule:
A function is increasing when and decreasing when .
Let's find where :
Since for all , we need to solve:
This gives us or
When analyzing where a function is increasing or decreasing, focus on where the first derivative changes sign.
Testing regions:
- For : and , so , meaning
- For : and , so , meaning
- For : and , so , meaning
Therefore:
- is increasing for
- is decreasing for
- is increasing for
A function is concave up when and concave down when .
From our second derivative:
Since for all , we need to solve :
Testing regions:
- For : , so
- For : , so
- For : , so
Therefore:
- is concave up for
- is concave down for
- is concave up for
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
We are given the rate at which the radius is changing:
(The rate is negative because the radius is decreasing).
We need to find the rates at which the surface area and the volume are changing at the instant when the radius is cm.
That is, we need to find and when .
The formulas for the surface area and volume of a sphere with radius are:
Surface Area:
Volume:
Now, we differentiate both formulas with respect to time , using implicit differentiation because , , and are all functions of .
For Surface Area :
For Volume :
When performing implicit differentiation with respect to time , remember that differentiating a term involving requires multiplying by . For example, . Similarly, and .
Substitute cm and cm/hr into the equation for :
The surface area is decreasing at a rate of square centimeters per hour.
Substitute cm and cm/hr into the equation for :
The volume is decreasing at a rate of cubic centimeters per hour.
Notice that the formula for is . Since the surface area , we can also write . This sometimes provides a shortcut if the surface area is already known or easily calculated.
When the radius is 10 cm, the surface area is decreasing at a rate of cm²/hr and the volume is decreasing at a rate of cm³/hr.
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Let's check what happens when we try to evaluate the limit directly:
As :
-
-
So we have the indeterminate form , which we can't evaluate directly.
To handle this indeterminate form, I'll define:
Taking the natural logarithm of both sides:
Using the property of logarithms:
Now we need to evaluate:
As :
-
-
So we have the indeterminate form , which means we can apply L'Hôpital's Rule.
Finding the derivatives:
Applying L'Hôpital's Rule:
For this new limit:
As :
-
-
We again have the indeterminate form , so we apply L'Hôpital's Rule again.
Finding the derivatives:
Applying L'Hôpital's Rule:
As :
-
So:
We found that , so:
For indeterminate forms like , always try the strategy of taking the natural logarithm first, then applying L'Hôpital's Rule to the resulting expression.
Therefore:
Exercise Tags
Tag:
Use the tag filtering feature on the course homepage to find all exercises with this tag.
Prerequisites for this Exercise
No prerequisite skills selected yet.
Let's define our variables:
- = side length of the square base (in feet)
- = height of the rectangular prism (in feet)
- = volume (in cubic feet)
The volume of the rectangular prism is:
Solving for :
The rectangular prism has 6 faces:
- 2 square faces (top and bottom) each with area
- 4 rectangular faces (sides) each with area
Total area of top and bottom = square feet
Total area of sides = square feet
Given:
- Cost of top and bottom material = per square foot
- Cost of side material = per square foot
Cost of top and bottom = dollars
Cost of sides = dollars
Total cost:
To minimize the cost, we take the derivative of with respect to and set it equal to zero:
Setting this equal to zero:
Using our earlier relation , we can calculate when :
Now let's find the ratio :
In optimization problems with cost functions, setting the derivative equal to zero and solving for the critical points is the key technique for finding minimum or maximum values.
Therefore, when the cost is minimized, the ratio of height to side length is: