Practice Final #3

Full Course
McGill University, MATH 140

Exam Settings

Show Tags
Unlock Course Now
Purchase course to access Discord community
Back to Course

Mixed Content

Mixed Content
A1
Find lim⁡x→5x2−8x+15x2−25. \lim_{x \to 5} \frac{x^2 - 8x + 15}{x^2 - 25}.

Exercise Tags

limits: general
parabolas

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Simplify the expression


To evaluate this limit, start by factoring both the numerator and the denominator. Factoring can often help us cancel out terms, especially if direct substitution initially results in an indeterminate form like 00\frac{0}{0}.

The numerator x2−8x+15 x^2 - 8x + 15 factors as:

x2−8x+15=(x−5)(x−3)
x^2 - 8x + 15 = (x - 5)(x - 3)



The denominator x2−25 x^2 - 25 is a difference of squares, which factors as:

x2−25=(x−5)(x+5)
x^2 - 25 = (x - 5)(x + 5)


So, the expression becomes:

(x−5)(x−3)(x−5)(x+5)
\frac{(x - 5)(x - 3)}{(x - 5)(x + 5)}


Step 2: Cancel common terms


Now, cancel the common factor (x−5) (x - 5) from both the numerator and the denominator:

(x−3)(x+5)
\frac{(x - 3)}{(x + 5)}


Step 3: Substitute the limit


Now that we’ve simplified the expression, we can substitute x=5 x = 5 directly:

5−35+5=210=15
\frac{5 - 3}{5 + 5} = \frac{2}{10} = \frac{1}{5}


Key Tip: When faced with indeterminate forms, factor and cancel common terms to simplify the expression.

15
\boxed{\frac{1}{5}}
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
15
\boxed{\frac{1}{5}}
A2
Find ddx(log⁡3(x)+4x−x2+17). \frac{d}{dx} \left( \log_3(x) + 4^x - x^2 + 17 \right).

Exercise Tags

differentiation: logarithmic
Differentiation: general

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Differentiate each term separately


To find the derivative, apply the rules of differentiation to each term individually. We’ll use the following key rules:

Derivative of log⁡a(x) \log_a(x) : 1xln⁡(a) \frac{1}{x \ln(a)} and Derivative of ax a^x : axln⁡(a) a^x \ln(a)

**Derivative of** log⁡3(x) \log_3(x) :

ddx(log⁡3(x))=1xln⁡(3)
\frac{d}{dx} \left( \log_3(x) \right) = \frac{1}{x \ln(3)}


**Derivative of** 4x 4^x :

ddx(4x)=4xln⁡(4)
\frac{d}{dx} \left( 4^x \right) = 4^x \ln(4)


**Derivative of** −x2 -x^2 :

ddx(−x2)=−2x
\frac{d}{dx} \left( -x^2 \right) = -2x


**Derivative of** 17 17 (a constant):

ddx(17)=0
\frac{d}{dx} \left( 17 \right) = 0


Step 2: Combine the results


Now, we can combine each of these derivatives to find the overall derivative:


ddx(log⁡3(x)+4x−x2+17)=1xln⁡(3)+4xln⁡(4)−2x
\begin{align*}
\frac{d}{dx} \left( \log_3(x) + 4^x - x^2 + 17 \right)
&= \frac{1}{x \ln(3)} \\
&\quad + 4^x \ln(4) - 2x
\end{align*}




1xln⁡(3)+4xln⁡(4)−2x\boxed{\frac{1}{x \ln(3)} + 4^x \ln(4) - 2x}
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
1xln⁡(3)+4xln⁡(4)−2x\boxed{\frac{1}{x \ln(3)} + 4^x \ln(4) - 2x}
A3
Find ddx(1+exx2+9). \frac{d}{dx} \left( \frac{1 + e^x}{x^2 + 9} \right).

Exercise Tags

quotient rule
Differentiation: general

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Recognize the need for the quotient rule


To differentiate 1+exx2+9 \frac{1 + e^x}{x^2 + 9} , we use the quotient rule, which states:

Quotient Rule: If f(x)=uv f(x) = \frac{u}{v} , then f′(x)=u′v−uv′v2 f'(x) = \frac{u'v - uv'}{v^2}

In this case:
- u=1+ex u = 1 + e^x
- v=x2+9 v = x^2 + 9

Step 2: Differentiate the numerator and denominator


**Derivative of** u=1+ex u = 1 + e^x :

u′=ddx(1+ex)=ex
u' = \frac{d}{dx} (1 + e^x) = e^x


**Derivative of** v=x2+9 v = x^2 + 9 :

v′=ddx(x2+9)=2x
v' = \frac{d}{dx} (x^2 + 9) = 2x


Step 3: Apply the quotient rule


Now, substitute u u , u′ u' , v v , and v′ v' into the quotient rule formula:



ddx(1+exx2+9)=(ex)(x2+9)−(1+ex)(2x)(x2+9)2
\frac{d}{dx} \left( \frac{1 + e^x}{x^2 + 9} \right) = \frac{(e^x)(x^2 + 9) - (1 + e^x)(2x)}{(x^2 + 9)^2}




Step 4: Simplify the expression (if possible)


Distribute ex e^x and 2x 2x :

=ex⋅x2+9ex−2x−2xex(x2+9)2
= \frac{e^x \cdot x^2 + 9e^x - 2x - 2x e^x}{(x^2 + 9)^2}


ex⋅x2+9ex−2x−2xex(x2+9)2
\boxed{\frac{e^x \cdot x^2 + 9e^x - 2x - 2x e^x}{(x^2 + 9)^2}}
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
ex⋅x2+9ex−2x−2xex(x2+9)2
\boxed{\frac{e^x \cdot x^2 + 9e^x - 2x - 2x e^x}{(x^2 + 9)^2}}
A4
Find the derivative of

sin⁡(e3x+17ln⁡(x2+1))
\sin \left( e^{3x} + 17 \ln(x^2 + 1) \right)

Exercise Tags

Differentiation: general
differentiation: logarithmic

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Recognize the need for the chain rule


To differentiate sin⁡(e3x+17ln⁡(x2+1)) \sin \left( e^{3x} + 17 \ln(x^2 + 1) \right) , we’ll apply the chain rule. The chain rule states:

Chain Rule: If f(x)=g(h(x)) f(x) = g(h(x)) , then f′(x)=g′(h(x))⋅h′(x) f'(x) = g'(h(x)) \cdot h'(x)

In this case:
- g(x)=sin⁡(x) g(x) = \sin(x)
- h(x)=e3x+17ln⁡(x2+1) h(x) = e^{3x} + 17 \ln(x^2 + 1)

Step 2: Differentiate the outer function


First, differentiate the outer function g(x)=sin⁡(x) g(x) = \sin(x) :

g′(h(x))=cos⁡(e3x+17ln⁡(x2+1))
g'(h(x)) = \cos \left( e^{3x} + 17 \ln(x^2 + 1) \right)


Step 3: Differentiate the inner function


Now, we differentiate the inner function h(x)=e3x+17ln⁡(x2+1) h(x) = e^{3x} + 17 \ln(x^2 + 1) :

**Derivative of** e3x e^{3x} :

ddx(e3x)=3e3x
\frac{d}{dx} \left( e^{3x} \right) = 3e^{3x}


**Derivative of** 17ln⁡(x2+1) 17 \ln(x^2 + 1) :

Using the chain rule again on ln⁡(x2+1) \ln(x^2 + 1) :

ddx(17ln⁡(x2+1))=17⋅1x2+1⋅2x=34xx2+1
\frac{d}{dx} \left( 17 \ln(x^2 + 1) \right) = 17 \cdot \frac{1}{x^2 + 1} \cdot 2x = \frac{34x}{x^2 + 1}


Combining these, we have:

h′(x)=3e3x+34xx2+1
h'(x) = 3e^{3x} + \frac{34x}{x^2 + 1}


Step 4: Apply the chain rule


Now, we can combine g′(h(x)) g'(h(x)) and h′(x) h'(x) to find the derivative:


ddx(sin⁡(e3x+17ln⁡(x2+1)))=
\frac{d}{dx} \left( \sin \left( e^{3x} + 17 \ln(x^2 + 1) \right) \right) =


cos⁡(e3x+17ln⁡(x2+1))⋅(3e3x+34xx2+1)
\cos \left( e^{3x} + 17 \ln(x^2 + 1) \right) \cdot
\left( 3e^{3x} + \frac{34x}{x^2 + 1} \right)


cos⁡(e3x+17ln⁡(x2+1))⋅(3e3x+34xx2+1)
\boxed{\cos \left( e^{3x} + 17 \ln(x^2 + 1) \right) \cdot \left( 3e^{3x} + \frac{34x}{x^2 + 1} \right)}





Prof's perspective


This question checks your ability to apply the chain rule in complex scenarios involving trigonometric, exponential, and logarithmic functions. The professor likely chose this question to ensure you can differentiate nested functions accurately, a skill that is crucial for handling advanced calculus problems.
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access





cos⁡(e3x+17ln⁡(x2+1))⋅(3e3x+34xx2+1)
\boxed{\cos \left( e^{3x} + 17 \ln(x^2 + 1) \right) \cdot \left( 3e^{3x} + \frac{34x}{x^2 + 1} \right)}


A5
Find

lim⁡x→2(tan⁡((x3−x2−x−2)πx2+17x−38))
\lim_{x \to 2} \left( \tan \left( \frac{(x^3 - x^2 - x - 2)\pi }{x^2 + 17x - 38} \right) \right)

Exercise Tags

factoring: grouping
unit circle values
limits: general

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Simplify the expression inside the tangent function


To evaluate this limit, start by simplifying the expression within the tangent function. We’ll try factoring the numerator and the denominator.
The numerator x3−x2−x−2 x^3 - x^2 - x - 2 can be factored by grouping terms.

Factoring by Grouping


To factor x3−x2−x−2 x^3 - x^2 - x - 2 , we group the terms in pairs:

x3−x2−x−2=(x3−x2)−(x+2)
x^3 - x^2 - x - 2 = (x^3 - x^2) - (x + 2)


Now, factor out x2 x^2 from the first group and factor out −1 -1 from the second group:

=x2(x−1)−1(x−1)
= x^2(x - 1) - 1(x - 1)


Now we have a common factor of (x−2) (x - 2) :

=(x−2)(x2+x+1)
= (x - 2)(x^2 + x + 1)


The denominator x2+17x−38 x^2 + 17x - 38 factors as:

x2+17x−38=(x−2)(x+19)
x^2 + 17x - 38 = (x - 2)(x + 19)


So, the expression becomes:

tan⁡((x−2)(x2+x+1)(x−2)(x+19)π)
\tan \left( \frac{(x - 2)(x^2 + x + 1)}{(x - 2)(x + 19)} \pi \right)


Step 2: Cancel common terms


Now, cancel the common factor (x−2) (x - 2) from both the numerator and the denominator:

tan⁡(x2+x+1x+19π)
\tan \left( \frac{x^2 + x + 1}{x + 19} \pi \right)


Step 3: Substitute the limit


Now that we’ve simplified the expression, we can substitute x=2 x = 2 directly:

tan⁡(22+2+12+19π)=
\tan \left( \frac{2^2 + 2 + 1}{2 + 19} \pi \right) =


tan⁡(4+2+121π)=
\tan \left( \frac{4 + 2 + 1}{21} \pi \right) =


tan⁡(721π)=
\tan \left( \frac{7}{21} \pi \right) =


tan⁡(π3)
\tan \left( \frac{\pi}{3} \right)


Tip: You need to know the unit circle and the values of common trigonometric functions at special angles, such as π3 \frac{\pi}{3} , to solve problems like this.


Since tan⁡(π3)=3 \tan \left( \frac{\pi}{3} \right) = \sqrt{3} , we have:

3
\boxed{\sqrt{3}}


Prof's perspective


This question is designed to test your ability to handle limits involving trigonometric functions, especially by simplifying rational expressions through factoring. The professor likely included this question to emphasize the importance of **factoring and cancelling terms** before evaluating limits, a common approach in calculus to avoid indeterminate forms.
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
3
\boxed{\sqrt{3}}
A6
Compute the derivative of

x3+17x+9
x^3 + 17x + 9


from first principles, i.e., from the definition of the derivative as a limit.

Exercise Tags

differentiation: first principles

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Set up the definition of the derivative


The derivative of f(x)=x3+17x+9 f(x) = x^3 + 17x + 9 from first principles is defined as:

f′(x)=lim⁡h→0f(x+h)−f(x)h
f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h}


Step 2: Substitute f(x+h) f(x + h) and f(x) f(x)


In this case, f(x)=x3+17x+9 f(x) = x^3 + 17x + 9 , so let’s compute f(x+h) f(x + h) :



f(x+h)=(x+h)3+17(x+h)+9f(x + h) = (x + h)^3 + 17(x + h) + 9




Expanding (x+h)3 (x + h)^3 :

(x+h)3=x3+3x2h+3xh2+h3
(x + h)^3 = x^3 + 3x^2h + 3xh^2 + h^3


Then:

f(x+h)=x3+3x2h+3xh2+h3+17x+17h+9
f(x + h) = x^3 + 3x^2h + 3xh^2 + h^3 + 17x + 17h + 9


Now, substitute into the definition:


f′(x)=lim⁡h→0(x3+3x2h+3xh2+h3+17x+17h+9)−(x3+17x+9)h
f'(x) = \lim_{h \to 0} \frac{\left( x^3 + 3x^2h + 3xh^2 + h^3 + 17x + 17h + 9 \right) - \left( x^3 + 17x + 9 \right)}{h}


Step 3: Simplify the expression


Cancel out the terms x3 x^3 , 17x 17x , and 9 9 in the numerator:


=lim⁡h→03x2h+3xh2+h3+17hh
= \lim_{h \to 0} \frac{3x^2h + 3xh^2 + h^3 + 17h}{h}



Now, factor h h from each term in the numerator:

=lim⁡h→0h(3x2+3xh+h2+17)h
= \lim_{h \to 0} \frac{h(3x^2 + 3xh + h^2 + 17)}{h}


Cancel h h in the numerator and denominator:

=lim⁡h→0(3x2+3xh+h2+17)
= \lim_{h \to 0} \left( 3x^2 + 3xh + h^2 + 17 \right)


Step 4: Take the limit as h→0 h \to 0


Now, substitute h=0 h = 0 :

f′(x)=3x2+17
f'(x) = 3x^2 + 17


3x2+17
\boxed{3x^2 + 17}
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
The derivative is:

3x2+17
\boxed{3x^2 + 17}


but you have to show all your steps for full marks.
A7
Find the domain of the function

ln⁡(cot⁡−1(x2)−π6)\ln \left( \cot^{-1}(x^2) - \frac{\pi}{6} \right)

Exercise Tags

logarithms
find the domain
inverse trig functions
unit circle values

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Determine the domain of the logarithmic function


For the natural logarithm ln⁡(y) \ln(y) , the argument y y must be greater than zero. In this case that means:

cot⁡−1(x2)−π6>0
\cot^{-1}(x^2) - \frac{\pi}{6} > 0


which is therefore our first condition that we need to satisfy.

Step 2: Analyze the domain of cot⁡−1(x2) \cot^{-1}(x^2)


The function cot⁡−1(x2) \cot^{-1}(x^2) is defined for all x x because x2≥0 x^2 \geq 0 for all real values of x x .

So there are no added restrictions on the domain from cot⁡−1(x2) \cot^{-1}(x^2) .

You need to know the graph of cot⁡(x)\cot(x). You can use this for finding info about cot⁡−1(x)\cot^{-1}(x) by switching axis.




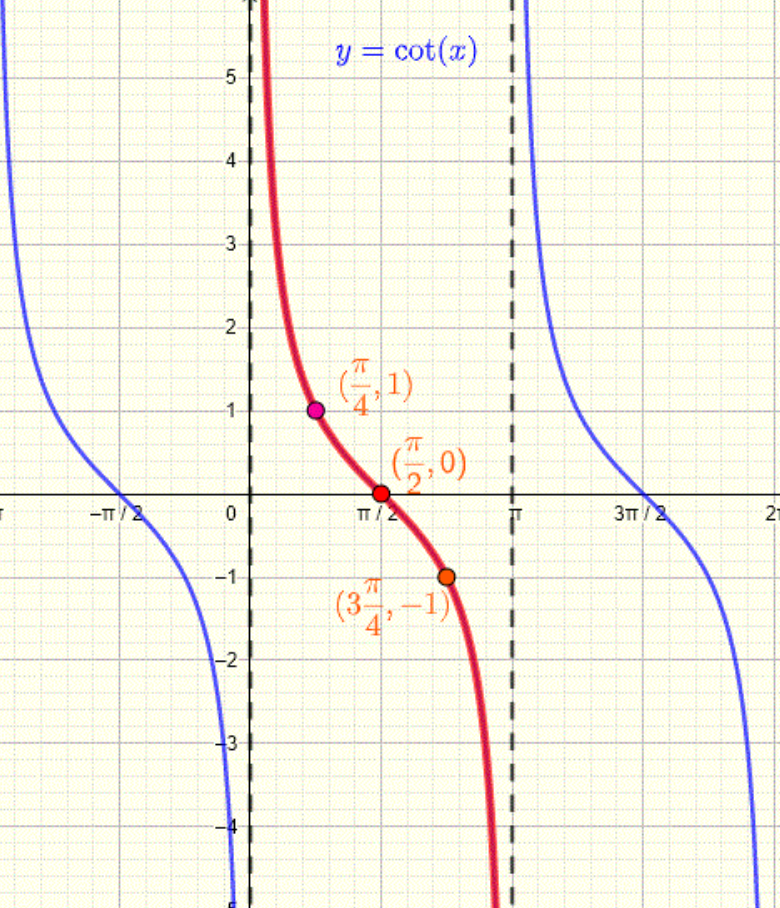
cotangent graph

Figure: graph of cotangent



You also will need to know the unit circle values.


Step 3: Set up the inequality


To satisfy the condition for the logarithm, we need:

cot⁡−1(x2)−π6>0
\cot^{-1}(x^2) - \frac{\pi}{6} > 0


This simplifies to:

cot⁡−1(x2)>π6
\cot^{-1}(x^2) > \frac{\pi}{6}


Step 4: Solve for x x


Now, we find the values of x x such that cot⁡−1(x2)>π6 \cot^{-1}(x^2) > \frac{\pi}{6} .

Since cot⁡−1(x2) \cot^{-1}(x^2) decreases as x2 x^2 increases, we need:

x2<cot⁡(π6)
x^2 < \cot\left( \frac{\pi}{6} \right)


From the unit circle, we know cot⁡(π6)=3 \cot\left( \frac{\pi}{6} \right) = \sqrt{3} , so:

x2<3
x^2 < \sqrt{3}


Taking the square root of both sides:

∣x∣<34
|x| < \sqrt[4]{3}


Thus, the domain of the function is:

−34<x<34
\boxed{-\sqrt[4]{3} < x < \sqrt[4]{3}}


Prof's perspective


This problem tests your understanding of the domain of composite functions, especially when involving inverse trigonometric functions and logarithms. The professor likely included this question to ensure you know how to work with domain restrictions and analyze inequalities involving inverse trigonometric expressions.
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
−34<x<34
\boxed{-\sqrt[4]{3} < x < \sqrt[4]{3}}
A8
Compute the following limit

lim⁡x→1(4tan⁡−1(x)−πx2+8x−9)
\lim_{x \to 1} \left( \frac{4 \tan^{-1}(x) - \pi}{x^2 + 8x - 9} \right)

Exercise Tags

inverse trig functions
L'hopitals rule
limits: general

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Substitute x=1 x = 1 to check for indeterminate form


First, let’s substitute x=1 x = 1 into the expression:

Numerator:

4tan⁡−1(1)−π
4 \tan^{-1}(1) - \pi


=4⋅π4−π=π−π=0
= 4 \cdot \frac{\pi}{4} - \pi = \pi - \pi = 0


Denominator:

12+8⋅1−9=1+8−9=0
1^2 + 8 \cdot 1 - 9 = 1 + 8 - 9 = 0


Since both the numerator and denominator are zero, we have an indeterminate form 00\frac{0}{0}. Therefore, we can apply **L'Hôpital's Rule**, which states:

L'Hôpital's Rule: If lim⁡x→af(x)g(x)=00 \lim_{x \to a} \frac{f(x)}{g(x)} = \frac{0}{0} or ±∞±∞ \frac{\pm \infty}{\pm \infty} , then lim⁡x→af(x)g(x)=lim⁡x→af′(x)g′(x) \lim_{x \to a} \frac{f(x)}{g(x)} = \lim_{x \to a} \frac{f'(x)}{g'(x)} , provided the limit on the right exists.

Step 2: Differentiate the numerator and denominator


**Differentiate the numerator** 4tan⁡−1(x)−π 4 \tan^{-1}(x) - \pi :

Tip: Remember the derivatives of inverse trigonometric functions! For tan⁡−1(x) \tan^{-1}(x) , the derivative is 11+x2 \frac{1}{1 + x^2} .

ddx(4tan⁡−1(x)−π)
\frac{d}{dx} \left( 4 \tan^{-1}(x) - \pi \right)


=4⋅11+x2=41+x2
= 4 \cdot \frac{1}{1 + x^2} = \frac{4}{1 + x^2}


**Differentiate the denominator** x2+8x−9 x^2 + 8x - 9 :

ddx(x2+8x−9)=2x+8
\frac{d}{dx} \left( x^2 + 8x - 9 \right) = 2x + 8


Step 3: Apply L'Hôpital's Rule


Now, substitute these derivatives into the limit:

lim⁡x→141+x22x+8
\lim_{x \to 1} \frac{\frac{4}{1 + x^2}}{2x + 8}


Substitute x=1 x = 1 :

=41+122⋅1+8=4210=210=15
= \frac{\frac{4}{1 + 1^2}}{2 \cdot 1 + 8} = \frac{\frac{4}{2}}{10} = \frac{2}{10} = \frac{1}{5}


15\boxed{\frac{1}{5}}
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
15\boxed{\frac{1}{5}}
A9
Let f(x)=(x2−6x+9)ex f(x) = (x^2 - 6x + 9)e^x .

Exercise Tags

Curve Sketching

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access

Sub-questions:

A9 Part a)
Find the maximum of f(x) f(x) in the interval [0,2][0, 2].

Exercise Tags

find critical numbers
maximizing and minimizing
find max/min values

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Determine the critical points


To find the maximum, we need to calculate the derivative f′(x) f'(x) and set it to zero to find critical points. We’ll use the product rule since f(x) f(x) is the product of (x2−6x+9) (x^2 - 6x + 9) and ex e^x .

**Using the product rule**:

f′(x)=ddx((x2−6x+9)ex)
f'(x) = \frac{d}{dx} \left( (x^2 - 6x + 9)e^x \right)


Let:
- u=x2−6x+9 u = x^2 - 6x + 9
- v=ex v = e^x

Then:
- u′=2x−6 u' = 2x - 6
- v′=ex v' = e^x

So,

f′(x)
f'(x)

=u′v+uv′
= u'v + uv'

=(2x−6)ex+(x2−6x+9)ex
= (2x - 6)e^x + (x^2 - 6x + 9)e^x


Combine terms:


f′(x)=((2x−6)+(x2−6x+9))ex
f'(x) = \left( (2x - 6) + (x^2 - 6x + 9) \right) e^x



Simplify the expression inside the parentheses:

f′(x)=(x2−4x+3)ex
f'(x) = \left( x^2 - 4x + 3 \right) e^x


Now, set f′(x)=0 f'(x) = 0 :

(x2−4x+3)ex=0
(x^2 - 4x + 3)e^x = 0


Since ex≠0 e^x \neq 0 , we only need to solve:

x2−4x+3=0
x^2 - 4x + 3 = 0


Factoring gives:

(x−1)(x−3)=0
(x - 1)(x - 3) = 0


So, x=1 x = 1 and x=3 x = 3 . However, since we are only interested in the interval [0,2][0, 2], we discard x=3 x = 3 and keep x=1 x = 1 .

Step 2: Evaluate f(x) f(x) at the endpoints and the critical point


Now, evaluate f(x) f(x) at x=0 x = 0 , x=1 x = 1 , and x=2 x = 2 :

**At** x=0 x = 0 :

f(0)=(02−6⋅0+9)e0=9⋅1=9
f(0) = (0^2 - 6 \cdot 0 + 9)e^0 = 9 \cdot 1 = 9


**At** x=1 x = 1 :

f(1)=(12−6⋅1+9)e1=(1−6+9)e=4e
f(1) = (1^2 - 6 \cdot 1 + 9)e^1 = (1 - 6 + 9)e = 4e


**At** x=2 x = 2 :

f(2)=(22−6⋅2+9)e2=(4−12+9)e2=1⋅e2=e2
f(2) = (2^2 - 6 \cdot 2 + 9)e^2 = (4 - 12 + 9)e^2 = 1 \cdot e^2 = e^2


Step 3: Determine the maximum value


Now, compare the values at x=0 x = 0 , x=1 x = 1 , and x=2 x = 2 :

f(0)=9,f(1)=4e,f(2)=e2
f(0) = 9, \quad f(1) = 4e, \quad f(2) = e^2


Since e2≈7.39 e^2 \approx 7.39 and 4e≈10.87 4e \approx 10.87 , the maximum value occurs at x=1 x = 1 with f(1)=4e f(1) = 4e .

4e
\boxed{4e}


Prof's perspective


This question is designed to test your understanding of the product rule, as well as evaluating functions at critical points and endpoints to find absolute maximums or minimums. The professor likely included this question to ensure you can handle more complex functions and apply calculus principles over a specified interval.
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
4e
\boxed{4e}
A9 Part b)
Find where f(x) f(x) is concave down.

Exercise Tags

concavity
graphing

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Find the second derivative of f(x) f(x)


To determine where f(x) f(x) is concave down, we need to find the second derivative f′′(x) f''(x) and determine where it is negative.

Recall that f(x)=(x2−6x+9)ex f(x) = (x^2 - 6x + 9)e^x . We already found the first derivative:

f′(x)=(x2−4x+3)ex
f'(x) = \left( x^2 - 4x + 3 \right) e^x


Now, we’ll differentiate f′(x) f'(x) again to find f′′(x) f''(x) , using the product rule.

Let:
- u=x2−4x+3 u = x^2 - 4x + 3
- v=ex v = e^x

Then:
- u′=2x−4 u' = 2x - 4
- v′=ex v' = e^x

Applying the product rule:

f′′(x)=u′v+uv′
f''(x) = u'v + uv'


Substitute u u , u′ u' , v v , and v′ v' :



f′′(x)=(2x−4)ex+(x2−4x+3)ex
f''(x) = (2x - 4)e^x + (x^2 - 4x + 3)e^x



Combine terms:

f′′(x)=(2x−4+x2−4x+3)ex
f''(x) = \left( 2x - 4 + x^2 - 4x + 3 \right)e^x


Simplify inside the parentheses:

f′′(x)=(x2−2x−1)ex
f''(x) = \left( x^2 - 2x - 1 \right) e^x


Step 2: Determine where f′′(x)<0 f''(x) < 0


To find where f(x) f(x) is concave down, we need f′′(x)<0 f''(x) < 0 .

Since ex>0 e^x > 0 for all x x , the sign of f′′(x) f''(x) depends only on x2−2x−1 x^2 - 2x - 1 :

x2−2x−1<0
x^2 - 2x - 1 < 0


Solve this inequality by finding the roots of x2−2x−1=0 x^2 - 2x - 1 = 0 using the quadratic formula:

x=2±(2)2−4⋅1⋅(−1)2⋅1
x = \frac{2 \pm \sqrt{(2)^2 - 4 \cdot 1 \cdot (-1)}}{2 \cdot 1}


=2±4+42
= \frac{2 \pm \sqrt{4 + 4}}{2}


=2±222
= \frac{2 \pm 2\sqrt{2}}{2}


=1±2
= 1 \pm \sqrt{2}


Step 3: Test intervals


Now, we test the sign of x2−2x−1 x^2 - 2x - 1 in the intervals around these roots, namely, in the intervals (−∞,1−2) (-\infty, 1 - \sqrt{2}) , (1−2,1+2) (1 - \sqrt{2}, 1 + \sqrt{2}) , and (1+2,∞) (1 + \sqrt{2}, \infty) .

** Interval 1: (−∞,1−2) (-\infty, 1 - \sqrt{2})
Choose a test point x=−2 x = -2 in this interval.

Substitute x=−2 x = -2 into x2−2x−1 x^2 - 2x - 1 :

(−2)2−2(−2)−1=4+4−1=7
(-2)^2 - 2(-2) - 1 = 4 + 4 - 1 = 7


Since 7>0 7 > 0 , the function is positive in this interval.

**Interval 2: (1−2,1+2) (1 - \sqrt{2}, 1 + \sqrt{2})
Choose a test point x=1 x = 1 in this interval.

Substitute x=1 x = 1 into x2−2x−1 x^2 - 2x - 1 :

(1)2−2(1)−1=1−2−1=−2
(1)^2 - 2(1) - 1 = 1 - 2 - 1 = -2


Since −2<0 -2 < 0 , the function is negative in this interval.

** Interval 3: (1+2,∞) (1 + \sqrt{2}, \infty)
Choose a test point x=3 x = 3 in this interval.

Substitute x=3 x = 3 into x2−2x−1 x^2 - 2x - 1 :

(3)2−2(3)−1=9−6−1=2
(3)^2 - 2(3) - 1 = 9 - 6 - 1 = 2


Since 2>0 2 > 0 , the function is positive in this interval.


Conclusion



Since the function is negative in the interval (1−2,1+2) (1 - \sqrt{2}, 1 + \sqrt{2}) , this is the interval where the function is concave down.

(1−2,1+2)
\boxed{(1 - \sqrt{2}, 1 + \sqrt{2})}
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
(1−2,1+2)
\boxed{(1 - \sqrt{2}, 1 + \sqrt{2})}
A9 Part c)
c) Find the horizontal asymptote(s) of f(x) f(x) .

Exercise Tags

graphing
asymptotes

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Analyze the behavior of f(x) f(x) as x→∞ x \to \infty and x→−∞ x \to -\infty


To find horizontal asymptotes, we examine the behavior of f(x)=(x2−6x+9)ex f(x) = (x^2 - 6x + 9)e^x as x x approaches positive and negative infinity.

**As x→∞ x \to \infty :**

The exponential term ex e^x grows extremely fast as x→∞ x \to \infty . Therefore, f(x) f(x) will also grow without bound because of ex e^x , making f(x)→∞ f(x) \to \infty .

**Conclusion**: There is no horizontal asymptote as x→∞ x \to \infty .

**As x→−∞ x \to -\infty :**

When x→−∞ x \to -\infty , ex e^x approaches 0 0 because exponential functions decay towards zero for large negative inputs. Thus:

f(x)=(x2−6x+9)ex≈0 as x→−∞
f(x) = (x^2 - 6x + 9)e^x \approx 0 \text{ as } x \to -\infty


Conclusion


Since f(x) f(x) approaches 0 0 as x→−∞ x \to -\infty , there is a horizontal asymptote at:

y=0
\boxed{y = 0}
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
y=0
\boxed{y = 0}
A10
Let f(x)=5x10+3x3−1 f(x) = 5x^{10} + 3x^3 - 1 .

Exercise Tags

Intermediate Value Theorem

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access

Sub-questions:

A10 Part a)
Show that f(x) f(x) has at least one zero in [0,1].[0, 1].

Exercise Tags

Intermediate Value Theorem

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Use the Intermediate Value Theorem (IVT)


To show that f(x) f(x) has at least one zero in [0,1][0, 1], we can apply the **Intermediate Value Theorem**, which states:

Intermediate Value Theorem: If f f is continuous on [a,b][a, b] and f(a) f(a) and f(b) f(b) have opposite signs, then there exists at least one c∈(a,b) c \in (a, b) such that f(c)=0 f(c) = 0 .

Step 2: Check the continuity of f(x) f(x)


The function f(x)=5x10+3x3−1 f(x) = 5x^{10} + 3x^3 - 1 is a polynomial, and polynomials are continuous everywhere. Therefore, f(x) f(x) is continuous on [0,1][0, 1].

Step 3: Evaluate f(x) f(x) at the endpoints


Evaluate f(0) f(0) :

f(0)=5⋅010+3⋅03−1=−1
f(0) = 5 \cdot 0^{10} + 3 \cdot 0^3 - 1 = -1


Evaluate f(1) f(1) :

f(1)
f(1)

=5⋅110+3⋅13−1
= 5 \cdot 1^{10} + 3 \cdot 1^3 - 1

=5+3−1=7
= 5 + 3 - 1 = 7

=7
= 7


Step 4: Apply the Intermediate Value Theorem


Since f(0)=−1 f(0) = -1 and f(1)=7 f(1) = 7 , f(0) f(0) and f(1) f(1) have opposite signs. By the Intermediate Value Theorem, there must be at least one c∈(0,1) c \in (0, 1) such that f(c)=0 f(c) = 0 .

Therefore, f(x) has at least one zero in [0,1].
\boxed{\text{Therefore, } f(x) \text{ has at least one zero in } [0, 1].}
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
See walkthrough
A10 Part b)
Show that this root is unique, i.e., that f(x) f(x) cannot have more than one zero in the same interval.

Exercise Tags

Intermediate Value Theorem

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Check the sign of f′(x) f'(x) in the interval [0,1][0, 1]


To show that f(x) f(x) has only one zero in [0,1][0, 1], we can examine the behavior of the function by analyzing its derivative f′(x) f'(x) . If f′(x) f'(x) does not change sign in [0,1][0, 1], then f(x) f(x) is either strictly increasing or strictly decreasing on that interval, implying at most one zero.

Given:

f(x)=5x10+3x3−1
f(x) = 5x^{10} + 3x^3 - 1


Differentiate f(x) f(x) to find f′(x) f'(x) :

f′(x)=10⋅5x9+3⋅3x2=50x9+9x2
\begin{align*}
f'(x) &= 10 \cdot 5x^9 + 3 \cdot 3x^2 \\
&= 50x^9 + 9x^2
\end{align*}


Step 2: Analyze the sign of f′(x) f'(x) in [0,1][0, 1]


Since f′(x)=50x9+9x2 f'(x) = 50x^9 + 9x^2 , note that each term 50x9 50x^9 and 9x2 9x^2 is non-negative for x≥0 x \geq 0 . Therefore, f′(x)≥0 f'(x) \geq 0 for all x∈[0,1] x \in [0, 1] , and f′(x)=0 f'(x) = 0 only at x=0 x = 0 .

Since f′(x)≥0 f'(x) \geq 0 on [0,1][0, 1], f(x) f(x) is non-decreasing on this interval. This implies that f(x) f(x) can have at most one zero in [0,1][0, 1], as a non-decreasing function cannot cross the x-axis more than once without changing direction.

Conclusion


Since f(x) f(x) is continuous on [0,1][0, 1] and has a zero in this interval (from part (a)), and since f(x) f(x) is non-decreasing on [0,1][0, 1], we conclude that the zero is unique.

The root of f(x) in [0,1] is unique.
\boxed{\text{The root of } f(x) \text{ in } [0, 1] \text{ is unique.}}
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
See walkthrough
A11
Find the derivative of

cosh⁡(x3sec⁡(x))
\cosh \left( \sqrt[3]{x} \sec(x) \right)

Exercise Tags

hyperbolic trig functions
Differentiation: general

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Recognize the need for the chain rule


To differentiate cosh⁡(x3sec⁡(x)) \cosh \left( \sqrt[3]{x} \sec(x) \right) , we apply the chain rule. Let:

f(x)=cosh⁡(g(x))whereg(x)=x3sec⁡(x)
f(x) = \cosh \left( g(x) \right) \quad \text{where} \quad g(x) = \sqrt[3]{x} \sec(x)


The derivative of f(x)=cosh⁡(g(x)) f(x) = \cosh(g(x)) is:


Tip: Remember that the derivative of cosh⁡(x) \cosh(x) is sinh⁡(x) \sinh(x) . For functions of the form cosh⁡(g(x)) \cosh(g(x)) , use the chain rule: f′(x)=sinh⁡(g(x))⋅g′(x) f'(x) = \sinh(g(x)) \cdot g'(x) .


f′(x)=sinh⁡(g(x))⋅g′(x)
f'(x) = \sinh(g(x)) \cdot g'(x)


Step 2: Differentiate g(x)=x3sec⁡(x) g(x) = \sqrt[3]{x} \sec(x)


We need to find g′(x) g'(x) by differentiating g(x)=x1/3sec⁡(x) g(x) = x^{1/3} \sec(x) using the product rule.

Let:
- u=x1/3 u = x^{1/3}
- v=sec⁡(x) v = \sec(x)

Then:
- u′=13x−2/3=13x2/3 u' = \frac{1}{3} x^{-2/3} = \frac{1}{3x^{2/3}}
- v′=sec⁡(x)tan⁡(x) v' = \sec(x) \tan(x)

Using the product rule:

g′(x)=u′v+uv′
g'(x) = u'v + uv'


Breaking down the calculation:


g′(x)=13x2/3sec⁡(x)+x1/3sec⁡(x)tan⁡(x)=sec⁡(x)3x2/3+x1/3sec⁡(x)tan⁡(x)
\begin{align}
g'(x) &= \frac{1}{3x^{2/3}} \sec(x) + x^{1/3} \sec(x) \tan(x) \\
&= \frac{\sec(x)}{3x^{2/3}} + x^{1/3} \sec(x) \tan(x)
\end{align}



Step 3: Substitute g(x) g(x) and g′(x) g'(x) into f′(x) f'(x)


Now we can write the derivative of f(x)=cosh⁡(x3sec⁡(x)) f(x) = \cosh \left( \sqrt[3]{x} \sec(x) \right) :


sinh⁡(x3sec⁡(x))⋅(sec⁡(x)3x2/3+x1/3sec⁡(x)tan⁡(x))
\boxed{\sinh \left( \sqrt[3]{x} \sec(x) \right) \cdot \left( \frac{\sec(x)}{3x^{2/3}} + x^{1/3} \sec(x) \tan(x) \right)}

PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access

sinh⁡(x3sec⁡(x))⋅(sec⁡(x)3x2/3+x1/3sec⁡(x)tan⁡(x))
\boxed{ \sinh \left( \sqrt[3]{x} \sec(x) \right) \cdot \left( \frac{\sec(x)}{3x^{2/3}} + x^{1/3} \sec(x) \tan(x) \right)}

A12
An object moves on the curve defined by the implicit relation

4x3+y2+5x2y=0
4x^3 + y^2 + 5x^2 y = 0


When reaching x=1 x = 1 and y=−4 y = -4 , the rate of change in the x x -direction is given by dxdt=3 \frac{dx}{dt} = 3 . What is dydt \frac{dy}{dt} at this point?

Exercise Tags

relates rates
differentiation: implicit

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Differentiate both sides with respect to t t


To find dydt \frac{dy}{dt} , we need to implicitly differentiate the equation with respect to t t , applying the chain rule to each term.

Starting with:

4x3+y2+5x2y=0
4x^3 + y^2 + 5x^2 y = 0


Differentiate each term with respect to t t :

ddt(4x3)+ddt(y2)+ddt(5x2y)=0
\frac{d}{dt}(4x^3) + \frac{d}{dt}(y^2) + \frac{d}{dt}(5x^2 y) = 0


Step 2: Differentiate each term


**First term**: ddt(4x3) \frac{d}{dt}(4x^3)

=4⋅3x2⋅dxdt=12x2dxdt= 4 \cdot 3x^2 \cdot \frac{dx}{dt} = 12x^2 \frac{dx}{dt}

**Second term**: ddt(y2) \frac{d}{dt}(y^2)

=2ydydt= 2y \frac{dy}{dt}

**Third term**: ddt(5x2y) \frac{d}{dt}(5x^2 y)

Using the product rule:

=5(2xdxdt⋅y+x2dydt)=10xydxdt+5x2dydt
\begin{align}
&= 5 \left( 2x \frac{dx}{dt} \cdot y + x^2 \frac{dy}{dt} \right) \\
&= 10x y \frac{dx}{dt} + 5x^2 \frac{dy}{dt}
\end{align}



Step 3: Substitute into the differentiated equation


Now, combine all terms:


12x2dxdt+2ydydt+10xydxdt+5x2dydt=0
12x^2 \frac{dx}{dt} + 2y \frac{dy}{dt} + 10x y \frac{dx}{dt} + 5x^2 \frac{dy}{dt} = 0



Group the dydt \frac{dy}{dt} terms:

(2y+5x2)dydt=−(12x2+10xy)dxdt
(2y + 5x^2) \frac{dy}{dt} = - (12x^2 + 10x y) \frac{dx}{dt}


Step 4: Substitute values for x=1 x = 1 , y=−4 y = -4 , and dxdt=3 \frac{dx}{dt} = 3


Substitute x=1 x = 1 , y=−4 y = -4 , and dxdt=3 \frac{dx}{dt} = 3 :
(2(−4)+5(1)2)dydt=−(12(1)2+10(1)(−4))⋅3
\begin{align}
&(2(-4) + 5(1)^2) \frac{dy}{dt} = \\
&- \left( 12(1)^2 + 10(1)(-4) \right) \cdot 3
\end{align}



Simplify each term:

(−8+5)dydt=−(12−40)⋅3
(-8 + 5) \frac{dy}{dt} = - (12 - 40) \cdot 3


−3dydt=−(−28)⋅3-3 \frac{dy}{dt} = -(-28) \cdot 3

−3dydt=84-3 \frac{dy}{dt} = 84

Solve for dydt \frac{dy}{dt} :

dydt=84−3=−28
\frac{dy}{dt} = \frac{84}{-3} = -28


dydt=−28\boxed{\frac{dy}{dt} = -28}
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
dydt=−28\boxed{\frac{dy}{dt} = -28}
A13
Find the derivative of

ln⁡(x9(x4+6)3x8+20x2+7)
\ln \left( \frac{x^9 (x^4 + 6)^3}{x^8 + 20x^2 + 7} \right)


when x=1.x=1.

Exercise Tags

Differentiation: general
differentiation: logarithmic
logarithms

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Use the logarithmic properties


We can use the property ln⁡(ab)=ln⁡(a)−ln⁡(b) \ln \left( \frac{a}{b} \right) = \ln(a) - \ln(b) to separate the terms:


ln⁡(x9(x4+6)3x8+20x2+7)=
\ln \left( \frac{x^9 (x^4 + 6)^3}{x^8 + 20x^2 + 7} \right) =

ln⁡(x9(x4+6)3)−
\ln \left( x^9 (x^4 + 6)^3 \right) -

ln⁡(x8+20x2+7)
\ln \left( x^8 + 20x^2 + 7 \right)



Now, apply the property ln⁡(ab)=ln⁡(a)+ln⁡(b) \ln(ab) = \ln(a) + \ln(b) to the first term:

ln⁡(x9(x4+6)3)=ln⁡(x9)+ln⁡((x4+6)3)
\ln \left( x^9 (x^4 + 6)^3 \right) = \ln(x^9) + \ln((x^4 + 6)^3)


Use the property ln⁡(an)=nln⁡(a) \ln(a^n) = n \ln(a) :

ln⁡(x9)=9ln⁡(x)
\ln(x^9) = 9 \ln(x)


ln⁡((x4+6)3)=3ln⁡(x4+6)
\ln((x^4 + 6)^3) = 3 \ln(x^4 + 6)


Thus, the expression becomes:

9ln⁡(x)+3ln⁡(x4+6)−ln⁡(x8+20x2+7)
9 \ln(x) + 3 \ln(x^4 + 6) - \ln(x^8 + 20x^2 + 7)


Step 2: Differentiate each term


Now, we differentiate each term separately. We will use basic derivative rules.

**Differentiate 9ln⁡(x) 9 \ln(x) :**

ddx(9ln⁡(x))=9x
\frac{d}{dx}(9 \ln(x)) = \frac{9}{x}


**Differentiate 3ln⁡(x4+6) 3 \ln(x^4 + 6) :**

Using the chain rule:

ddx(3ln⁡(x4+6))=3x4+6⋅ddx(x4+6)=3x4+6⋅4x3=12x3x4+6
\begin{align*}
\frac{d}{dx}(3 \ln(x^4 + 6)) &= \frac{3}{x^4 + 6} \cdot \frac{d}{dx}(x^4 + 6) \\
&= \frac{3}{x^4 + 6} \cdot 4x^3 \\
&= \frac{12x^3}{x^4 + 6}
\end{align*}


**Differentiate −ln⁡(x8+20x2+7) - \ln(x^8 + 20x^2 + 7) :**

Using the chain rule:


ddx(−ln⁡(x8+20x2+7))=\frac{d}{dx} \left( - \ln(x^8 + 20x^2 + 7) \right) =
−1x8+20x2+7⋅ddx(x8+20x2+7)- \frac{1}{x^8 + 20x^2 + 7} \cdot \frac{d}{dx}(x^8 + 20x^2 + 7)



Now differentiate x8+20x2+7 x^8 + 20x^2 + 7 :

ddx(x8+20x2+7)=8x7+40x\frac{d}{dx}(x^8 + 20x^2 + 7) = 8x^7 + 40x

So the derivative of the third term is:

−8x7+40xx8+20x2+7- \frac{8x^7 + 40x}{x^8 + 20x^2 + 7}

Step 3: Combine all terms


Now, we combine the derivatives:

9x+12x3x4+6−8x7+40xx8+20x2+7\frac{9}{x} + \frac{12x^3}{x^4 + 6} - \frac{8x^7 + 40x}{x^8 + 20x^2 + 7}

Step 4: Evaluate the derivative at x=1 x = 1


Substitute x=1 x = 1 into the expression for u′(x) u'(x) and u(x) u(x) :

**First term:**

91=9\frac{9}{1} = 9

**Second term:**

12(1)3(1)4+6=127\frac{12(1)^3}{(1)^4 + 6} = \frac{12}{7}

**Third term:**

8(1)7+40(1)(1)8+20(1)2+7=8+401+20+7=4828=127\frac{8(1)^7 + 40(1)}{(1)^8 + 20(1)^2 + 7} = \frac{8 + 40}{1 + 20 + 7} = \frac{48}{28} = \frac{12}{7}

Now combine everything:

9+127−127=99 + \frac{12}{7} - \frac{12}{7} = 9

9\boxed{9}
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
9\boxed{9}
A14
The graph of the curve defined by the implicit equation

3y3−2xy=x23y^3 - 2xy = x^2

is given.
Current Exercise Image

Exercise Tags

Curve Sketching

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access

Sub-questions:

A14 Part a)
Find dydx \frac{dy}{dx} .

Exercise Tags

differentiation: implicit

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Implicitly differentiate both sides with respect to x x


We start with the implicit equation:

3y3−2xy=x2
3y^3 - 2xy = x^2


Differentiate both sides with respect to x x . For terms involving y y , we will use the chain rule because y y is a function of x x .

ddx(3y3)−ddx(2xy)=ddx(x2)
\frac{d}{dx}(3y^3) - \frac{d}{dx}(2xy) = \frac{d}{dx}(x^2)


**First term**: ddx(3y3) \frac{d}{dx}(3y^3)

Using the chain rule:

ddx(3y3)=9y2⋅dydx
\frac{d}{dx}(3y^3) = 9y^2 \cdot \frac{dy}{dx}


**Second term**: ddx(2xy) \frac{d}{dx}(2xy)

Using the product rule:

ddx(2xy)=2(xddx(y)+yddx(x))=2(xdydx+y)
\frac{d}{dx}(2xy) = 2 \left( x \frac{d}{dx}(y) + y \frac{d}{dx}(x) \right) = 2 \left( x \frac{dy}{dx} + y \right)


**Third term**: ddx(x2) \frac{d}{dx}(x^2)

ddx(x2)=2x\frac{d}{dx}(x^2) = 2x

Now, putting everything together:

9y2⋅dydx−2(xdydx+y)=2x
9y^2 \cdot \frac{dy}{dx} - 2 \left( x \frac{dy}{dx} + y \right) = 2x


Step 2: Solve for dydx \frac{dy}{dx}


Distribute the −2 -2 :

9y2⋅dydx−2x⋅dydx−2y=2x
9y^2 \cdot \frac{dy}{dx} - 2x \cdot \frac{dy}{dx} - 2y = 2x


Now group terms involving dydx \frac{dy}{dx} :

(9y2−2x)dydx=2x+2y
(9y^2 - 2x) \frac{dy}{dx} = 2x + 2y


Solve for dydx \frac{dy}{dx} :

dydx=2x+2y9y2−2x
\boxed{\frac{dy}{dx} = \frac{2x + 2y}{9y^2 - 2x}}
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
dydx=2x+2y9y2−2x
\boxed{\frac{dy}{dx} = \frac{2x + 2y}{9y^2 - 2x}}
A14 Part b)
Find the equation in the form y=mx+c y = mx + c of the tangent line at (−3,1) (-3, 1) .

Exercise Tags

point slope form

Tag:

Use the tag filtering feature on the course homepage to find all exercises with this tag.

View Tag Filter

Prerequisites for this Exercise

No prerequisite skills selected yet.

PREMIUM WALKTHROUGH

Unlock Premium Content

Get instant access to detailed walkthroughs, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
Step 1: Use the derivative from part (a)


From part (a), we found the derivative of the curve to be:

dydx=2x+2y9y2−2x
\frac{dy}{dx} = \frac{2x + 2y}{9y^2 - 2x}


We need to find the slope of the tangent line at (−3,1) (-3, 1) .

Substitute x=−3 x = -3 and y=1 y = 1 into the derivative:

dydx=2(−3)+2(1)9(1)2−2(−3)
\frac{dy}{dx} = \frac{2(-3) + 2(1)}{9(1)^2 - 2(-3)}


Simplify:

dydx=−6+29+6=−415
\frac{dy}{dx} = \frac{-6 + 2}{9 + 6} = \frac{-4}{15}


Thus, the slope of the tangent line at (−3,1) (-3, 1) is m=−415 m = \frac{-4}{15} .

Step 2: Use the point-slope form to find the equation of the tangent line


The point-slope form of the equation of a line is:

y−y1=m(x−x1)
y - y_1 = m(x - x_1)


Substitute the point (−3,1) (-3, 1) and the slope m=−415 m = \frac{-4}{15} :

y−1=−415(x−(−3))
y - 1 = \frac{-4}{15}(x - (-3))


Simplify:

y−1=−415(x+3)
y - 1 = \frac{-4}{15}(x + 3)


Step 3: Convert to slope-intercept form


Now, expand the equation:

y−1=−415x−45
y - 1 = \frac{-4}{15}x - \frac{4}{5}


Add 1 to both sides to solve for y y :

y=−415x−45+1
y = \frac{-4}{15}x - \frac{4}{5} + 1


Simplify:

y=−415x+15
y = \frac{-4}{15}x + \frac{1}{5}


Thus, the equation of the tangent line is:

y=−415x+15
\boxed{y = \frac{-4}{15}x + \frac{1}{5}}
PREMIUM SOLUTION

Unlock Premium Content

Get instant access to detailed solutions, step-by-step explanations, and exclusive learning materials.

Unlock Now
Secure & Instant Access
y=−415x+15
\boxed{y = \frac{-4}{15}x + \frac{1}{5}}